 własnie jest ich od groma
za każdym razem jak sinx −> 0 masz ln (0+) = −∞ ... i masz asymptotę pionową
własnie jest ich od groma
za każdym razem jak sinx −> 0 masz ln (0+) = −∞ ... i masz asymptotę pionową
| π | ||
Ekstrema też istnieją: w | +2kπ | |
| 2 |
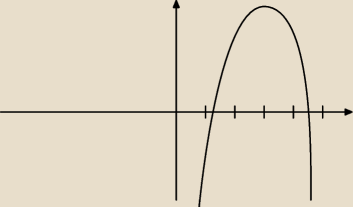 Funkcja będzie wyglądać mniej więcej tak? Wtedy by się zgadzało, tylko nie wiem jak wyliczyć
maksimum.
Funkcja będzie wyglądać mniej więcej tak? Wtedy by się zgadzało, tylko nie wiem jak wyliczyć
maksimum.
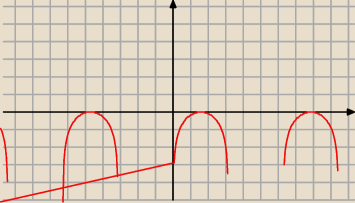 Tak wygląda wykres funkcji (tej ukośnej kreski nie powinno być)
y=lnsinx
Tak wygląda wykres funkcji (tej ukośnej kreski nie powinno być)
y=lnsinx
 Tylko jak to zapisać? Powinno być:?
y= logx − 1/6x2 − 1/180x4 + 0(x6) = logx − 5,5555 * 10−3 * x4 − 1,6666 * 10−1 * x2 +
0(x6)
Tak mi wyszło z kalkulatora:
http://wims.unice.fr/wims/wims.cgi?session=O81633918B.1&lang=en&cmd=reply&module=tool%2Fanalysis%2Ffunction.en&fn=ln%28sinx%29&show=subst&substitute=&show=deriv1&show=dev¢er=0&dev_order=5&ileft=&iright=&show=curve&left=&right=&lower=&upper=&show=points&pleft=&pright=&num_precision=12&format=t
Tylko jak to zapisać? Powinno być:?
y= logx − 1/6x2 − 1/180x4 + 0(x6) = logx − 5,5555 * 10−3 * x4 − 1,6666 * 10−1 * x2 +
0(x6)
Tak mi wyszło z kalkulatora:
http://wims.unice.fr/wims/wims.cgi?session=O81633918B.1&lang=en&cmd=reply&module=tool%2Fanalysis%2Ffunction.en&fn=ln%28sinx%29&show=subst&substitute=&show=deriv1&show=dev¢er=0&dev_order=5&ileft=&iright=&show=curve&left=&right=&lower=&upper=&show=points&pleft=&pright=&num_precision=12&format=t