matematykaszkolna.pl
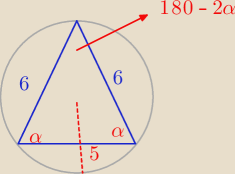
Planimetria Radek: rysunek Ramie trójkąta równoramiennego ma długość 6. Promień okręgu opisanego na tym trójkącie ma długość 5. Oblicz długość podstawy tego trójkąta Ja robiłem tak
6 
=10
sinα 
10sinα=6
 3 
sinα=
 5 
 4 
cosα=
 5 
 4 
62=62+x2−(2*6*x*
)
 5 
 48 
36=36+x2−
x
 5 
 48 
x2−
x=0 /5
 5 
5x2−48x=0 Δ=2304 √Δ=48
 48 
x1=
 5 
i taka jest odpowiedź ale czemu cosα dodatni skoro może być kąt rozwarty i wtedy cosα jest ujemny
16 gru 22:19
matyk: Z danych w zadaniu wynika, że nie może być rozwartokątny
16 gru 22:24
sushi_ gg6397228: przeciez α nie moze byc wiecej niz 90 stopni
16 gru 22:26
Eta: Trójkąt nie może mieć dwu kątów rozwartych!
16 gru 22:34
Radek: No tak to się zgadza. Ale skąd mam wiedzieć, że on ma już kąt rozwarty ?
16 gru 22:35
Eta: No chciałeś,żeby α −− był kątem rozwartym A takie kąty są dwa przy podstawie tego trójkąta ...... więc .......
16 gru 22:40
Radek:
16 gru 22:42
Radek: Ale ja nie wiem czy one nie są wszystkie ostre emotka ?
16 gru 22:52
Radek: Podbijam !
17 gru 20:19
Radek: emotka
17 gru 21:00
utem: 2*α<180⇔ α<90
17 gru 21:06
Eta: Kąt γ też nie może być rozwartym , bo wtedy z tw. cosinusów : |AB|2 = 62+62 +2*6*6*cosγ ⇒ |AB|>10, a najdłuższą cięciwą jest średnica tego okręgu : 2r= 10 Jasne już?
17 gru 21:16
Radek: Mniej więcej, temat już ogarnięty, ale dziękuję emotka
17 gru 21:18