Obliczyć granicę. Charles:

	1
lim(1−		)2n , gdzie n→∞
	n2

Charles: taki poziom widnieje na tym forum, że sam doszedłem jak to zrobić... Mianowicie e⁰ = 1 Przez 2,5 godziny, żeby nikt nie wiedział jak to policzyć − żal.

Bogdan: Dzień dobry. Charles − to jest forum, którego uczestnikami są uczniowie szkół gimnazjalnych i średnich, zaglądają czasami tu również studenci i jeśli na forum jest student lub osoba potrafiąca, a przede wszystkim chcąca pomóc, to przekaże wskazówki lub rozwiązanie zadania z materiału akademickiego. Nikt nie ma obowiązku udzielać pomocy, nie można więc formułować opinii w rodzaju: "nikt tego nie umie", "nikt tego nie wie". Może nikomu nie chciało się odpowiadać na Twoje zadanie? Skoro sam sobie poradziłeś, to od tego należało zacząć i nie wrzucać zadania na forum. Używając Twojego obraźliwego tonu powiem Ci tak − żal, że 2,5 godziny rozwiązywałeś banalne dla studenta zadanie.

tim: Witaj Bogdanie. Dzisiaj trochę będę

Bogdan: Witaj Tim. Spróbuj Timie rozmieścić w wierzchołkach 55−kąta liczby 1, 2, 3, 4 tak, by nie sąsiadowały ze sobą liczby jednakowe oraz 1 z 4 oraz 2 z 3.

Bogdan:

	1
Pokażę, jak łatwa była granica lim (1 −		)2n dla n→∞
	n2

	1		1
(1 −		)2n = [ (1 +		)−n2 ] = e−2/n → e0 = 1
	n2		−n2

tim: Wiem, że się nie da. Ale jest nieskończenie wiele (tzn ogromna ilość) takich kombinacji i wszystkich nie wypiszę np. 124312134343212434212434213... 124312431243... 12121212...

Bogdan: timie, nie masz wypisywać wszystkich, ponumeruj wierzchołki, wstaw jedną z liczb: 1, 2, 3 lub 4 w nr 1, sprawdź, co możesz wstawić w wierzchołki o nr parzystych, a co w pozostałe wierzchołki.

tim: Hmmm.. nr1 = 1 lub 4 nr2 = 2 lub 3 nr3 = 1 lub 4 nr4 = 2 lub 3 nr5 = 1 lub 4 ALBO nr1 = 2 lub 3 nr2 = 1 lub 4 nr3 = 2 lub 3 nr4 = 1 lub 4 O to chodzi? Oo

Bogdan: Zobacz timie, jakie liczby spotkają się w wierzchołkach nr 55 i 1.

tim: 1 z 1 1 z 4 4 z 4 4 z 1 lub 2 z 2 2 z 3 3 z 3 3 z 2 One dają w sumie 5. Eureka?

tim: A tak zbaczając z tematu: fajny jest matematyczny program Derive 6, choć nie produkują już go, można ściągnąć demo...

Bogdan: Tim − teraz wychodzę, wrócę wieczorem

tim: Ja zostaję na straży

tim: I wgl jak ja ci się odwdzięczę? Odpowiedz potem

Charles: Bogdan: Używając Twojego obraźliwego tonu powiem Ci tak − żal, że 2,5 godziny rozwiązywałeś banalne dla studenta zadanie. Po 1 nie studiuje − jestem uczniem 2 klasy LO. PS. Jestem ciekaw Twoich kwalifikacji.. ; )

tim: Oj zdziwisz sie..

tim: I jedno z następnych pytań, w czym tak ładnie zrobiłeś do pdfa?...

Bogdan: timie, korzystam z programu PDF Creator, który tworzy wirtualną drukarkę, po utworzeniu dokumentu wybieram opcję DRUKUJ, wybieram tę wirtualną drukarkę i dokument zostaje zapisany w formacie PDF.

tim: Ok, mam na kompie, ale gdzie piszesz? Odpowiedz na wcześniejsze pytania.

Bogdan: Do [Charles]] − zadania dotyczące granic funkcji, w tym granic ciągów jeszcze niedawno znajdowały się w programie nauczania szkoły średniej. Teraz niestety nie ma już analizy matematycznej na tym poziomie kształcenia, jeśli jednak sam, jak widzę, zająłeś się tym działem matematyki, to należy Ci się uznanie, co nie zmienia mojego niemiłego wrażenia o Twojej pogardliwej opinii o naszym forum. Na temat moich kwalifikacji nie wypowiadam się. Pozdrawiam

Bogdan: Pisałem maila do Ciebie w Wordzie 2007. A za co chcesz się Timie odwdzięczać, nie ma za co, z przyjemnością wymieniłem z Tobą matematyczne maile

tim: Ale jeszcze nie koniec! ... Jeszcze czworościan i chyba już finish.

Bogdan: Timie − nie odpuszczasz i to mi się podoba. Spróbuj jednak na razie sam, potem się włączę do Twoich przemyśleń o czworościanie.

tim: Łatwo mówić.. , został tydzień, a ja MUSZĘ wysłać. Jakby co termin mija 26 pazdziernika (muszę mieć napisane i zostawione na poczcie), ja myślę dalej, zapisuję to co mam, i tkwię dalej.

tim: Jeszcze Cię muszę podręczyć... Ale nie bądź zły. Z czego stwierdzić, w osiemnastokącie foremnym, że bok zielony i fioletowy (pionowy) są równoległe (patrz rysunek na poczcie)... Musisz powiedzieć, co mogę dla Ciebie zrobić w zamian.

tim: Tak apropos jakieś rozmnożenie MAGICow...

Bogdan: Cześć Tim, pobaw się miarami kątów w tym 18−kącie. Na rewanż przyjdzie czas, może za 18 lat

tim: Ok, ale będę pamiętał . Jeszcze nie koniec więc możesz chcieć więcej

Bogdan: Poczekam Tim, aż będziesz kimś sławnym, znanym, ważnym. Poproszę Ciebie wówczas o autograf

tim: Ha, ha bardzo śmieszne.

tim: Więc doszedłem do wniosku, że jeden z boków osiemnastokąta jest równoległy do zielonego pionowego odcinka. I czy teraz mogę napisać, że coś o przesunięciu może... Już nie mam siły.

Bogdan: Pożyjemy, zobaczymy. Może się okazać, że Twój autograf będzie cenną zdobyczą Sądząc po Twoich dotychczasowych osiągnięciach, jest to bardzo prawdopodobne.

Bogdan: W chwilach, gdy tracę wątek podczas rozwiązywania jakiegoś problemu lub zadania, gdy brakuje mi pomysłów, gdy jestem jakimś zagadnieniem zmęczony − odkładam sprawę na 1 dzień i staram się przez ten czas o tym nie myśleć.

tim: Łatwo Ci mówić.....

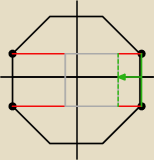
tim: Jeszcze mam pomysł skorzystania z symetryczności (jak na rysunku wyżej) i wynika, że te punkty są względem siebie symetryczne i odcinki między nimi równoległe. Teraz możemy np. wykorzystać przesunięcie równoległe. I mamy równoległość danych boków?

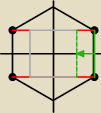
Bogdan: Tak Timie, dobry pomysł, ale upewnij się, czy badasz ośmiokąt, czy sześciokąt. Weź co trzeci wierzchołek − co wychodzi?

tim: Tak, wiem, że sześciokąt. Tu źle coś wyszło.

tim:

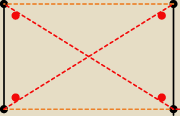
tim: A może można od razu skorzystać z tego, że przeciwległe boki sześciokąta są równoległe. Czarne są równoległe. Tam są kąty proste (kąty oparte na promieniu). I z tego wynika, że to jest prostokąt, i boki pomarańczowe też są równe.