Punkty A=(2,-6), C=(4,8) są przeciwległymi wierzchołkami rombu ABCD o boku długo kamczatka: Punkty A=(2,−6), C=(4,8) są przeciwległymi wierzchołkami rombu ABCD o boku długości 10. Wyznacz współrzędne pozostałych wierzchołków tego rombu. Środek S rombu S=(3,1) i nie wiem jak to wyliczyć dalej.

matyk: Robisz tak. Piszesz równanie okręgu o środku w punkcie A i promieniu 10 oraz o środku w punkcie C i promieniu 10. Punkty wspólne tych okręgów to pozostałe wierzchołki rombu

Hajtowy: B=(10;0)

Piotr 10: Można też inaczej Napisz równanie prostej AC Napisz równanie prostej BD prostopadłej do prostej AC i przechodzącej przez punkt S Skorzystaj z faktu, że IABI=10, a więc wylicz współrzędne punktu B za pomocą prostej BD ze zmienną x

kamczatka: dobra dzięki.

kamczatka: wyszło mi 50y²+40y 5²+4y y(5y+4) to podpunkt B by się zgadzał ale D się nie zgadza bo powinno wyjść (−4,2)

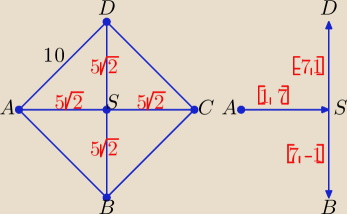
Bogdan: Inne rozwiązanie, a właściwie szkic rozwiązania z wykorzystaniem wektorów. Najpierw pokazujemy, że romb jest kwadratem: S = (3,1), |AS|² = 50, |SD|² = 10² − |AS|² = 50 = |AS|² Wektor AS^→= [1, 7], AS^→⊥SB^→ ⇒ SB^→= [7, −1], AS^→⊥SD^→ ⇒ SD^→= [−7, 1] B = (3 + 7), 1 − 1) = (10, 0), D = (3 − 7, 1 + 1) = (−4, 2)