tw sinusów
planimetria :
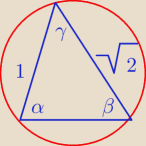
W okrąg o promieniu 1 wpisano trójkąt, którego dwa boki mają długość 1 i
√2 . Oblicz miary
kątów trójkąta.
2sinβ=1
sinβ=0,5
β=30
0
2sinα=
√2
α=45
o
γ=180−45−30=105
0
a w odpowiedziach mam jeszcze druga odpowiedź 15
o 30
o 135
o
16 gru 09:11
Radek: ?
16 gru 14:29
Radek: ?
16 gru 15:16
ICSP: ?
16 gru 15:23
Radek: Czemu w odpowiedziach są dwa wyniki?
16 gru 16:58
Bogdan:
i już wiadomo?
16 gru 17:11
Radek: Jeszcze nie do końca
16 gru 17:13
Radek: ?
16 gru 17:28
Bogdan:
α + β + γ = 180
o i α, β, γ ∊(0
o, 180
o)
| √2 | | 1 | |
| = sin45o = sin135o, |
| = sin30o = sin150o |
| 2 | | 2 | |
Rozpatrujemy wszystkie możliwe sytuacje (pokazałem je w poprzednim poście).
Otrzymujemy dwa rozwiązania.
16 gru 20:17
Radek:
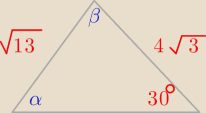
Panie Bogdanie, mam jeszcze problem z takim zadaniem.
Dwa boki trójkąta mają długość
√13 i 4
√3, a kąt przeciwległy krótszemu z nich ma miarę
30
0. Oblicz długość trzeciego boku
√13sinα=U{2
√3}
sinα=0,9607
Nie wiem czy to jest poprawnie jak do tej pory
?
16 gru 20:28
utem:
Tak.
16 gru 20:40
Radek: ale dobierając z tabeli sin 73
tego nie da sie obliczyć
16 gru 20:42
ICSP: a ktoś każe Ci to liczyć ?
16 gru 20:42
ICSP: Jedynka trygonometryczna?
Twierdzenie cosinusów ?
16 gru 20:42
Radek:
Znam i to i to..
16 gru 20:44
ICSP: To dlaczego nie wykorzystasz ?
16 gru 20:46
Radek:
Dobra już wiem jak zrobić
Dzięki
16 gru 20:46
utem:
Możesz też inaczej .
Oblicz wysokość opuszczoną z wierzchołka kąta β, potem oblicz dwie części podstawy.
16 gru 21:00
Radek:
(
√13)
2=(4
√3)
2+x
2−(2*4
√3x*cos30
0)
13=48+x
2−(12x)
13=48+x
2−12x
x
2−12+35=0
Δ=4
√Δ=2
x
2=7
ICSP mnie natchnął twierdzeniem cosinusów
16 gru 21:08
Bogdan:
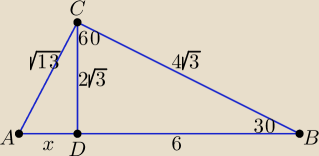
Albo korzystając z własności trójkąta prostokątnego o kątach ostrych 30
o i 60
o
i z twierdzenia Pitagorasa otrzymujemy:
| | 1 | |
|DB| = |CD|*√3 = |
| |BC|*√3 = 6, x = √13 − 12 = 1, |AB| = 1 + 6 = 7 |
| | 2 | |
16 gru 22:55
Radek: Dziękuję
17 gru 00:02