Punkt przegięcia funkcji, wklęsłość, wypukłość andrzej: y = 3x⁵ + 5x⁴ + 8x Czy ktoś może mnie nakierować jak obliczyć punkt przegięcia tej funkcji? Obliczam drugą pochodną, wychodzi mi równanie x³ +x² = 0, co teoretycznie daje nam PP dla x = 0 ⋀ x = −1 − funkcja ta jednak nie ma PP w x = 0. Co robię źle, czy zapominam o czymś co eliminuje ten punkt z rozwiązania? Mimo to w odpowiedziach mam że y^'' > 0 dla x ∊ (−1;0) ∪ (0;∞) czyli jednak to zero gdzieś tam musi się przewinąć

Bizon: ... zauważ co się dzieje z funkcją dla x=0

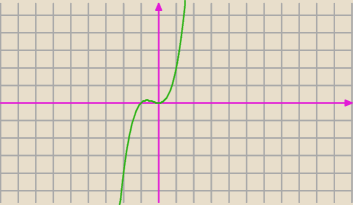
Bizon: ... przepraszam ...miało być " co się dzieje z drugą pochodną" a nie z funkcją. "zerowanie" drugiej pochodnej to tylko warunek konieczny ... ale nie dostateczny. Pochodna nie zmienia znaku ... więc?

andrzej: Rzeczywiście, w x = 0 funkcja się "odbija" od punktu, a nie przechodzi przez niego. Zwróciłem na to uwagę wcześniej, ale nie pomyślałem w ten sposób. Czyli punkty przegięcia mamy tylko tam gdzie druga pochodna zmienia znak i nie wystarczy że dany punkt jest jednym z pierwiastków tej pochodnej − zgadza się wszystko? Do tej pory jakoś zawsze w równaniach wychodziły mi sytuacje że pochodna zmieniała znak, dlatego taki wniosek jakoś wysunąłem, widać błędny

Bizon: f''(x)=x²(x+1) i dla x²(x+1)=0 x=0 jest pierwiastkiem podwójnym ... czyli "odbija" − A punkt przegięcia tylko kiedy spełnione są warunki konieczny i dostateczny −