ciung yolo: W trójkąt równoboczny o boku a wpisujemy okrąg. Następnie w każdym z trzech rogów wpisujemy kolejny okrąg styczny do wpisanego okręgu oraz do dwóch boków trójkąta. Postępujemy tak nieskończenie wiele razy. Oblicz sumę obwodów wpisanych okręgów. Jaką powierzchnię trójkąta zajmują wpisane koła?

yolo: jakies wskazowki? Ja doszedlem do wniosku ze suma obwodow to 2π(R+r1+r2+r3+...+rn). Ewentualnie suma promienia duzego kola + srednice wszystkich malych to odleglosc wierzcholka trojkata od srodka duzego kola

yolo: ludziee prosze o pomoc

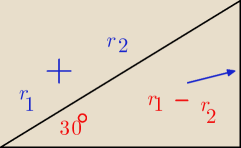
Panko: r₁ −−pierwszy promień r₁= a*√3/6 kolejne promienie powstają ze związku ( r_n−r_n+1 ) /( r_n+r_n+1 ) =sin30^◯ =1/2 stąd r_n = 3r_n+1 więc r₁=3r₂ , r₁=3²r₃ , r₁=3³r₄, .............( stosuj przy liczeniu obwodu) więc r₁²=3²r₂² , r₁²=3⁴r₃² , r₁=3⁶r₄² ,.. ( stosuj przy liczeniu pól), ......................................................... Suma długości okręgów tak wpisywanych każdy okrąg generuje 3 następców. S= 2*π*( r₁ + 3*r₂ + 3²*r₃ +3³*r₄+ .....) =?= 2π( r₁+ r₁ + r₁+....... r₁) jest to suma skończona gdy skończona jest liczba składników. Jeżeli wykonano n razy czynność wpisywania to suma łuków okręgów= 2π*n*r₁=2πn*a*√3/6 .................................................................. Teraz suma pól kół =P ( widać ,że nie może przekroczyć pola Δ); P=π(r₁² + 3r₂² +3²r₃² + 3³r₄²+...............) = π(r₁² + 3*(1/3²)*r₁² + 3²*(1/3⁴)r₁² + 3³*(1/3⁶)r₁²+.....)=π*r₁²*( 1+1/3+1/3² +1/3³+1/3⁴+....)=π*r₁²* (1/(1−1/3) )=(3/2)*π*r₁²=(3/2)*π*a²*(1/12)=(π/8)a² < Pole Δ ( niewiele)