Logarytmy
Tomkoon:
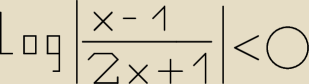
Witam mam problem z 8−mioma logarytmami:
1) log
3(3
x−8)=2−x
2) x
logx−2=1000
3)
√xlog√x=10
4) x
2logx10=10x
5) log
2x+log
3x+log
4x=1
6) log
x4+log
x264=5
7) log
4log
3log
2x=
12
8) rysunek na gorze xD
17 paź 00:25
Eta:
Kilka pomogę ( bo jest już dość późna godzina)
1/ załozenie: 3x −8 >0 => 3x >8 => x > log38 => x > 3log32
z def. log:
32−x= 3x −8 => 32*3−x = 3x −8
podstaw za 3x = t i 3−x= 1t
dokończ......
4/
alogab= b
założ. x >0
xlogx100= 10x => 100= 10x => x = 10
7/
zał. x >0
log3log2x = 41/2=2
log2x = 32 = 9
x = 29
no jeszcze jedno:
6/
założ, x >0 i x ≠1
logx 4*264 =5
x5 = 4*8*33 => x5 = 25*33 => x = 25√33
17 paź 01:04
Eta:
Wypiłam dobrą herbatkę

podaję jeszcze jedno rozwiązanie przed spankiem

np:
2/ założenie oczywiście: x>0
logarytmujemy równanie logarytmem dziesiętnym, otrzymujemy:
(logx − 2 )*logx = log1000 = 3
podstawiając za logx = t
t
2 −2t −3=0 Δ=16 t
1= 3 v t
2 = −1
więc: logx = 3 v logx= −1
to: x =1000 v x =
110
obydwa są rozwiazaniami bo x >0
no to teraz
3/ analogicznie:
zał. x>0
log
√x*log
√x= log10 => log
2√x= 1
....... dokończ , to już proste ...
Dobranoc Wszystkim

Do jutra

17 paź 01:37
Bogdan:
Pora spać. Dobranoc

17 paź 01:38
kasiek: x2log3x−3/2logx=√10
11 lis 13:02
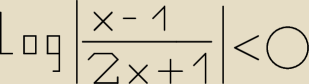 Witam mam problem z 8−mioma logarytmami:
1) log3(3x−8)=2−x
2) xlogx−2=1000
3) √xlog√x=10
4) x2logx10=10x
5) log2x+log3x+log4x=1
6) logx4+logx264=5
7) log4log3log2x=12
8) rysunek na gorze xD
Witam mam problem z 8−mioma logarytmami:
1) log3(3x−8)=2−x
2) xlogx−2=1000
3) √xlog√x=10
4) x2logx10=10x
5) log2x+log3x+log4x=1
6) logx4+logx264=5
7) log4log3log2x=12
8) rysunek na gorze xD
 podaję jeszcze jedno rozwiązanie przed spankiem
podaję jeszcze jedno rozwiązanie przed spankiem np:
2/ założenie oczywiście: x>0
logarytmujemy równanie logarytmem dziesiętnym, otrzymujemy:
(logx − 2 )*logx = log1000 = 3
podstawiając za logx = t
t2 −2t −3=0 Δ=16 t1= 3 v t2 = −1
więc: logx = 3 v logx= −1
to: x =1000 v x = 110
obydwa są rozwiazaniami bo x >0
no to teraz
3/ analogicznie:
zał. x>0
log√x*log√x= log10 => log2√x= 1
....... dokończ , to już proste ...
Dobranoc Wszystkim
np:
2/ założenie oczywiście: x>0
logarytmujemy równanie logarytmem dziesiętnym, otrzymujemy:
(logx − 2 )*logx = log1000 = 3
podstawiając za logx = t
t2 −2t −3=0 Δ=16 t1= 3 v t2 = −1
więc: logx = 3 v logx= −1
to: x =1000 v x = 110
obydwa są rozwiazaniami bo x >0
no to teraz
3/ analogicznie:
zał. x>0
log√x*log√x= log10 => log2√x= 1
....... dokończ , to już proste ...
Dobranoc Wszystkim  Do jutra
Do jutra 
