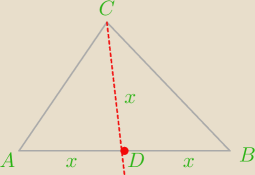
planimetria Radek: W trójkącie ABC bok AB jest dwa razy dłuższy od środkowej CD. Oblicz miarę kąta C Ale co dalej ? Proszę o wskazówkę ?

Radek: powinieneś mieć taką podpowiedź w trójkącie prostokątnym środkowa poprowadzona z wierzchołka kąta prostego jest promieniem okręgu opisanego na tym trójkącie

Radek: Jeżeli dobrze zrozumiałem zadanie

Radek: Imienniku ale skąd wiesz, że to trójkąt prostokątny ?

krystek: pob aw się kątami w trójkącie równoramiennym i kąt zewnętrzny jest równy sumie kątów wewnętrznych do niego nie przyległych

Radek: Dziękuję Pani za wskazówkę, może się uda

Radek: I lipa

zombi: Niech kąt CAD i ACD będą równe α (są takie same, ponieważ trójkąt ACD jest równoramienny) Natomiast kąty DCB i CBD będą równe β. Wobec tego: Kąt ADC = 180^o−2α Kąt BDC = 180^o−2β, ale suma kątów ADC + BDC = 180^o, czyli 360^o−2(α+β)=180^o ⇒ −2(α+β) = − 180^o ⇒ (α+β) = 90^o

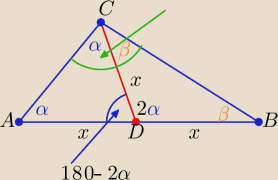
Eta: 2β+2α=180^o ⇒ α+β= 90^o =|∡ACB|

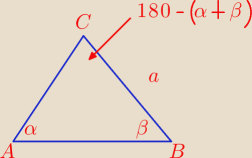
Radek: Dwa kąty trójkąta mają miary α i β, a bok przeciwległy do kątowi o mierze α ma długość a. Znajdź długości pozostałych boków

a		AC
	=
sinα		sinβ

	asinβ
AC=
	sinα

a		AB
	=
sinα		sin180−(α+β)

?

krystek: sin(180−(α+β))=sin(α+β)

Radek:

a		AB
	=
sinα		sin(a+β)

asin(α+β)=ABsinα

	asin(α+β)
AB=
	sinα

krystek: ok

Radek: Dziękuję Czyli nie ma potrzeby rozpisywać wzoru sin(α+β) ?

krystek: masz dane α iβ

Radek: No tak i ?

krystek: Co "i"?

Radek: sin[180⁰−(α+β)]=sin(α+β) wzory redukcyjne tak ?

krystek: 22:07