podstawą prostopadłościanu jest kwadrat o boku 2cm. krawędź boczna ma dł. √3 cm.
Znajdź miare kąta zawartego między krawędzią boczną a przekątną prostopadłościanu. Wynik podaj
z dokładnością do 1'.
podstawą prostopadłościanu jest kwadrat o boku 2cm. krawędź boczna ma dł. √3 cm.
Znajdź miare kąta zawartego między krawędzią boczną a przekątną prostopadłościanu. Wynik podaj
z dokładnością do 1'.
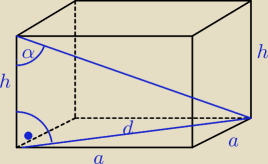 Dane: a = 2 cm α = ?
h = √3 cm
d = a√2 = 2√2
Dane: a = 2 cm α = ?
h = √3 cm
d = a√2 = 2√2
| d | |
= tgα | |
| h |
| 2√2 | 2√6 | 2 * 2,4495 | 4,8990 | |||||
tgα = | = | ≈ | = | = 1,633 | ||||
| √3 | 3 | 3 | 3 |


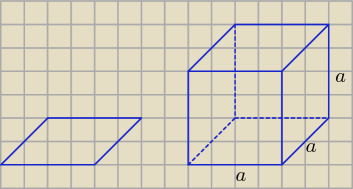 Poza zadaniem.
Jak narysować położony kwadrat, żeby wyglądał, jak położony kwadrat, a nie położony prostokąt ?
Należy narysować poziomy odcinek o długości parzystej liczbie jednostek, potem z końców
tego odcinka pod kątem 45o (po przekątnych kratek) odcinki o długości równej liczbie
przekątnych kratek, która jest połową liczby będącej długością poziomego odcinka.
Np. jeśli poziomy odcinek ma długość 4 jednostek, to ukośne odcinki mają długość 2 przekątnych
kratek.
Poza zadaniem.
Jak narysować położony kwadrat, żeby wyglądał, jak położony kwadrat, a nie położony prostokąt ?
Należy narysować poziomy odcinek o długości parzystej liczbie jednostek, potem z końców
tego odcinka pod kątem 45o (po przekątnych kratek) odcinki o długości równej liczbie
przekątnych kratek, która jest połową liczby będącej długością poziomego odcinka.
Np. jeśli poziomy odcinek ma długość 4 jednostek, to ukośne odcinki mają długość 2 przekątnych
kratek.

 Moja "połówka" −−− artysta malarz , więc się uzupełniamy : on maluje a ja "liczę"
Moja "połówka" −−− artysta malarz , więc się uzupełniamy : on maluje a ja "liczę" 

 Żegnam Was, dobrej nocy , do jutra.
Żegnam Was, dobrej nocy , do jutra.