Interpretacja geometryczna liczb zespolonych V.Abel: Witam, bardzo proszę o pomoc z tymi podpunktami: Narysuj na płaszczyźnie zespolonej:

	1+i
a) {z∊C: Arg(		= π2}
	z−3i

b) {z∊C: |z|²= 2are(z), a∊R} Pomocy, jak to rozpracować?

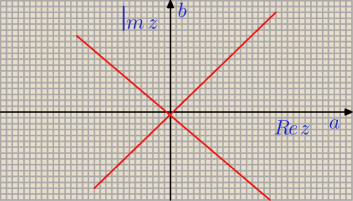
Panko: b) z=a+bi ⇒ IzI²=a² +b² =2*a*a ⇒ b²=a² b²=a² ⇔ b=a ⋁b=−a

V.Abel: Ok, z tym, że Ty podszedłeś do tego, że w podpunkcie b) a jest tym samym, co Rez, jednak wydaje mi się, że to jest ustalona stała (może się mylę, niech mnie ktoś poprawi!) A co z a) jakieś pomysły?

Krzysiek: a)arg(y)=π/2 zatem 'y' jest postaci: y=bi ,gdzie b>0

V.Abel: Dlaczego tak ?

Krzysiek: taka jest definicja argumentu, arg(y)=π/2, czyli kąt między osią Re(y) (dodatnią) a wektorem [a,b] (gdzie y=a+bi) jest równy 90 stopni, czyli punkt (a,b) znajduje się na dodatniej osi Im(y)

Panko: Jeżeli a to coś ustalonego to nazwijmy ją c żeby nie było kolizji wtedy a² +b² =ca ⇒ (a− c/2)² + b²= (c/2)² Jest to okrąg o środku O= ( c/2 , 0) i promieniu r =IcI/2

V.Abel: No ok, to która z Waszych wersji jest tu oczekiwana?

Panko: a) może tak ? arg ( 1+i ) = π/4; arg( z−3i) =φ teraz dzieląc obie postacie trygonometryczne liczb 1+i , z−3i dostajemy liczbe ktorej argu,entem jest arg ( (1+i) / (z−3i)) = π/4 −φ = π/4 stąd arg( z−3i) =0

Panko: Zaraz w punkcie a) jest 2a*Rez czyli korekta : a²+b² = 2ca ⇒ (a−c)² +b² = c² jest to okrąg o środku w punkcie O= ( c,0) i promieniu r=IcI o ile c≠a jeżeli c=a to para prostych .