Planimetria Radek:

	h
sinα=
	a

	h
a=
	sinα

	h
sinβ=
	b

	h
b=
	sinβ

	h		h
c2=(		)2+(		)2
	sinα		sinβ

	h2		h2
c2=		+		?
	sin2α		sin2β

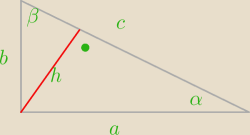
	h2sin2β+h2sin2β
c2=
	sin2β+sin2α

	h2(sin2α+sin2β)
c2=
	sin2β+sin2α

	h√sinα+sinβ		√sinβ−sinα
c=		*
	√sinβ+sinα		√sinβ−sinα

c=? dobrze myślę ?

Radek: ?

Radek: ?

Radek: ?

Eta: Napisz treść zadania !

Radek: Z tego wszystkiego zapomniałem treści: Jeden kąt ostry trójkąta prostokątnego ma miarę α, a wysokość poprowadzona z wierzchołka kąta prostego ma długość h. Oblicz długość pozostałych boków tego trójkąta

Eta:

h		h
	= sinα ⇒ b=
b		sinα

h		h
	= cosα ⇒ a=
a		cosα

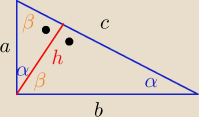
a		a		h		2h
	= sinα ⇒ c=		=		=
c		sinα		sinα*cosα		sin2α

i to wszystko

Radek: A może Pani dokończyć moje obliczenia ? Wydaję mi się, że nie popełniłem tam błędu w przekształceniach ?

Eta: wspólny mianownik to : sin²α*sin²β !

Eta: Czy Ty Radek nie widzisz,że to co napisałeś się uprości i c²= h² −−− a to jest sprzeczność

Radek: Jak bym to zauważył to bym się wgl nie pytał

Eta:

Eta: A wiesz,że sinβ= cosα ?

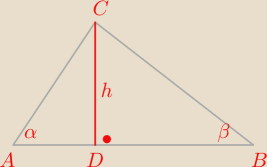
Radek: Wysokość poprowadzona z wierzchołka C trójkąta ABC ma długość h. Kąty BAC i ABC są ostre i mają odpowiednio miary α i β. Oblicz obwód trójkąta

	h
sinα=
	AC

	h
AC=
	sinα

	h
sinβ=
	CB

	h
CB=
	sinβ

DB=(CB)²−h²

	h
DB=(		2−h2
	sinα

	h2
DB=		−h2
	sin2α

	h2−h2sin2β
DB=
	sin2β

	h2(1−sin2β)
DB=
	sin2β

	h(1−sinβ)
DB=
	sinβ

AD=(AC)²−h²

	h
AD=		−h2
	sinα

	h2
AD=		−h2
	sin2α

	h2−h2sin2α
AD=
	sin2α

	h2(1−sin2α
AD=
	sin2α

	h(1−sinα
AD=
	sinα

OK ?

Radek: Tak wiem ta odpowiedź odnośnie pytania 23:16

Eta: Ech Radek .... ręce opadają Po co rozwiązywałeś zad poprzednie?

	1		1		1
L= h*(		+		+		)
	sinα		cosα		sinα*cosα

Radek: Ale to zadanie nie ma nic wspólnego z tym zadaniem które teraz wstawiłem... ?

Eta: Ojjj Radek, Radek Dane h i α , a=....... b=......... c=....... ( dokładnie to samo co poprzednio) Ob= a+b+c =......

Radek: Co poradzę, że nie ogarniam planimetrii i chcę się jej nauczyć ?

Eta: Nauczysz się, tylko włącz myślenie

Radek: Ok.

Eta: .......dobre na myślenie