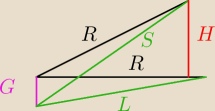
Oblicz wysokość w wilelokącie. Marek: Dzień dobry, mam takie zadanie do rozwiązania. Mamy dwa trójkąty o wspólnej podstawie G. Jeden o ramionach R i L. Drugi o ramionach S i R. Chciałbym wyliczyć wysokość H. Dane: G, R, L, S. Szukane H. Nie bardzo wiem jak się za to zabrać. z góry dziękuję. pozdrawiam

wredulus_pospolitus: ale to jest na płaszczyźnie czy przestrzeni jeżeli w przestrzeni to −−−− istnieje nieskończenie wiele rozwiązań

Marek: w płaszczyźnie oczywiście.

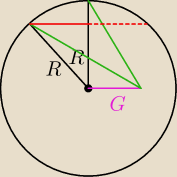
wredulus_pospolitus: jeżeli na płaszczyźnie to zauważ (patrz rysunek): wystarczy tylko wyznaczyć kąt pomiędzy bokami o długości 'R' i wyliczyć 'czerwoną' linię (połowa pełnej+przerywanej)

Marek: no tak. ale jak wyznaczyć ten kąt?

wredulus: Tw. Cosinusow

Marek: Nie mamy danej podstawy trójkąta o bokach R,R. I nie ma bardzo jak jej wyliczyć.

wredulus: Masz dane wymiary tych dwoch trojkatow ... wyznaczasz kat 'przy srodku okregu' dla tych dwoch t ojkatow ... kat pomiedzy bokami o dlugosci R,R to bedzie roznica tych dwoch wyliczonych katow

Marek: Teraz tak. czyli. Bierzemy trojkąt RGS S² = R²+G² − 2RGcosγ zatem cosγ=(S²−R²−G²)/2RG kąt γ jest to kąt (90+α) czyli cos(90+α)=(S²−R²−G²)/2RG zatem sinα=(G²+R²−S²)/2RG a sinα=H/R czyli H=(G²+R²−S²)/2G Wnioski H nie zależy od L pod warunkiem, że jest kąt prosty pomiędzy G a L. Będzie tak, Wredulusie? dzięki

wredulus: Oj nie nie nie .... jego sie obawialem ... ja narysowalem jeden trojkat prostokatny ... ale tak nie musi byc Wic nie musi zachodzic γ = 90+α

Marek: ale w moim przypadku jest 90 stopni. Zatem obliczenia są OK?

wredulus_pospolitus: jeżeli jest 90⁰ to ok tylko (jezeli nie masz podane) pokaz ze jest to 90^o (z pitagorasa najszybciej)

Marek: Coś mi cały czas nie pasowało. Zgubiłem minus. powinno być Bierzemy trojkąt RGS S² = R²+G² − 2RGcosγ zatem cosγ=(−S²+R²+G²)/2RG kąt γ jest to kąt (90+α) czyli cos(90+α)=(−S²+R²+G²)/2RG zatem sinα=(−G²−R²+S²)/2RG a sinα=H/R czyli H=(S²−R²−G²)/2G teraz jest OK. Bo tak zawsze wychodzilo mi na minusie