planimetriunia tangensior xd: W rombie o boku a i kącie ostrym alfa poprowadzono z wierzchołka kąta ostrego odcinki do przeciwległych boków tak, że podzieliły one romb na trzy części o równych polach. Oblicz długości każdego z tych odcinków. Plzzzzzz pomocy ;−−−−***************8

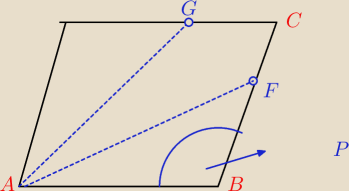
Panko: okazany kąt w przy wierzchołku B ma miare 180−α przyjmuję, że a długość boku rombu, wtedy IBFI = p*a gdzie p ∊(0,1) to część boku AC Pole ΔABF= 1/2 * a * p*a * sin(180−α) = 1/2*a²*psinα ma byc Pole ΔABF = 1/3 Pole rombu = 1/3 a² sinα z porównania 1/2*a²*p = 1/3 a² sinα ⇒ p=2/3 czyli IBFI = 2/3 *a stąd IAFI²= IABI² + IBFI² −2IABI*IBFI*cosα IAFI= √13/9a²−2/3a²cosα IAGI=IAFI stąd Pole czworokąta AFCG =1/3 Pola rombu

pigor: ..., lub z symetrii rombu względem przekątnej tu AC i warunków zadania chcemy aby P_ΔAFC= ¹₂P_ΔABF, co ma miejsce przy jednakowych wysokościach względem FC i BF, gdy podstawy |BF|=2|FC|= 2*¹₃a= ²₃a, wtedy |AF|²= a²+⁴₉a²−2*a*²₃cos(180^o−α)= ¹³₉a²+⁴₃a²cosα, czyli |AF|²= ¹₉a²(13+4cosα} ⇒ |AF|= |AG|= ¹₃a√13+4cosα . ...