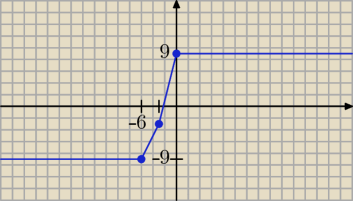
funkcja liniowa Garda: Dana jest funkcja f określona wzorem f(x)=lx+6l−2lxl+lx+3l, x należy do (−6;0). a) zapisz wzór tej funkcji bez użycia symbolu wartości bezwzględnej b) narysuj wykres tej funkcji c) podaj zbiór wartości funkcji f. Proszę o pomoc w tym zadaniu.

Bogdan: f(x) = lx+6l − 2lxl + lx+3l, Dla x∊(−∞, −6>: f(x) = −(x + 6) + 2x − (x + 3) ⇒ f(x) = −x − 6 + 2x − x − 3 ⇒ f(x) = −9; Dla x∊(−6, −3): f(x) = x + 6 + 2x − (x + 3) ⇒ f(x) = 3x + 6 − x − 3 ⇒ f(x) = 2x + 3; Dla x∊<−3, 0): f(x) = x + 6 + 2x + x + 3 ⇒ f(x) = 4x + 9; Dla x∊<0, +∞): f(x) = x + 6 − 2x + x + 3 ⇒ f(x) = 9 Na pytania zawarte w zadaniu postaraj się samodzielnie odpowiedzieć.

Garda: OK, tylko skąd się wzięły te wartości w nawiasach 'x należy' ? I jak to wszystko zostało obliczone, ktoś mi to objaśni krok po kroku?

Bogdan: To już jest krok po kroku.