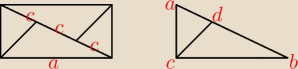
Podobienstwo Rosumad: 1) Prostopadłe poprowadzone z dwóch wierzchołków prostokąta na jego przekątną, dzielą ją na trzy równe części. Dłuższy bok prostokąta a= 4√2. Wyznacz pole tego prostokąta 2) Dany jest trójkąt prostokątny ABC, którego przyprostokątne |AC|=4 i |BC|= 4√3. Z wierzchołka kąta prostego C poprowadzono wysokość |CD|, wyznacz długość odcinka |AD|.

Rosumad: Zapomnialem oczywiscie poprosic o pomoc w rozwiazaniu w pierwszym poscie, przepraszam.

Rosumad: @bump

pigor: ..., np. tak : 1) niech x < a=4√2 − nieznana długość krótszego boku prostokąta; h długość odcinka ⊥ do przekątnej prostokąta, to P_p=4√2*x= ? − szukane jego pole, zatem z podobieństwa 3−ech trójkątów prostokątnych "w połowie" danego prostokąta masz np. :

c		h		x
	=		=		= t ⇒ c= h t i h= 2c t i x= 4√2 t ⇒
h		2c		4√2

⇒ c= 2ct² i x= 4√2t ⇒ 2t²=1 i x= 4√2t ⇒ √2t=1 i x= 4*1=4 < a, zatem P_p= 4√2*x= 4√2*4= 16√2 − szukane pole prostokąta .

Panko: a) Oznaczmy b brakujący bok w prostokącie , h pokazane wysokości ba=h* 3c − równość pól Δ; oraz h²= c*2c ⇒ba=3c*c√2 = 3√2c² przekątna prostokąta : a²+b² =9c² stąd a²+b²= 9* ba/3√2 a²+b² = 3/√2 * ba ⇒b²−12b+32=0 ⇒ b=8 lub b=4 Odp b= 4 Pole= 16√2

Rosumad: Dziekuje bardzo za pomoc.

pigor: ..., no to jeszcze np. tak : 2) z danych |ac|=4 i |bc|=4√3 i niech |ad|= x =? − szukana długość, to z tw. Pitagorasa |ab|²=4²+(4√3)²= 16+16*3= 4*16 ⇒ |ab|=2*4= 8, zatem |bd|= 8−x i podobieństwa ΔΔ−ów jak w zad. 1) : 8*|cd|=4*4√3 i |cd|²=x(8−x) ⇔ |cd|=2√3 i (2√3²=x(8−x) ⇒ x(8−x)=12 ⇔ ⇔ x(8−x)= 6*2 ⇔ x=|ad|=6 − szukana długość odcinka ad . ...

Rosumad: Mialbym jeszcze jedno pytanie, mianowicie: 2√2 = √4√2+b jak wyznaczyc "b"?

Rosumad: Nie wazne, dziekuje za pomoc, Panko i Pigor.

Eta:

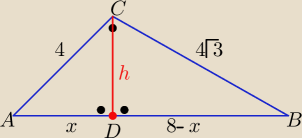
	1		1
|AB|= 8 P(ABC)=		*4*4√3= 8√3 i P=		*8*h =4h
	2		2

to h= 2√3 z tw. Pitagorasa x= √4²−(2√3)²= 2 |AD|= 2 i |DB|= 6