Asymptota funkcji
arcane: Bardzo proszę o sprawdzenie moich obliczeń, czy wszystko się zgadza?
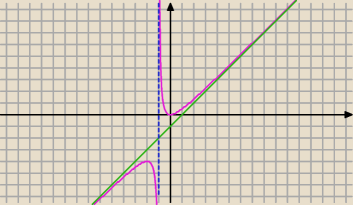
f(x)=x2/(x+1)
Df= R\{−1}
limx−> −1+ =+∞
limx−> −1− =−∞
x=−1 asymptota pionowa
asymptota pozioma:
limx−>+∞ x2/(x+1)= +∞
asymptota ukośna: y=ax+b
a=limx−>+∞ f(x)/x= limx−>+∞ x2/(x+1) * 1/x= limx−>+∞ x/(x+1)= 1
b= limx−>+∞ (f(x)−ax)= limx−>+∞ x2/(x+1) −x= −x/(x+1)= −1
12 gru 15:16
Aga1.:
Poprawny zapis wygląda tak.
| | x2 | | 1 | |
limx→−1− |
| =[ |
| ]=−∞ |
| | x+1 | | 0− | |
Reszta ok.
12 gru 16:35
arcane: Dziękuję bardzo.
Pozdrawiam
12 gru 16:41