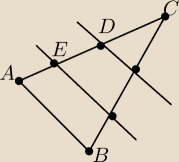
Pole trójkąta, pole koła - zadania Kropka: Rysunek schematyczny do zadania 1, od góry będzie P₁ (nie wiem, jak to zaznaczyć na rysunku). 1. Na boku trójkąta ABC zaznaczono punkty D, E w taki sposób, że |AE|=|ED|=|DC|. Przez punkty E, D przeprowadzono proste równoległe do boku AB, które podzieliły trójkąt na trzy rozłączne figury o polach równych odpowiednio P₁, P₂, P₃. Zatem: a) P₂ : P₃ = 1 : 2 b) P₂ : P₃ = 2 : 3 c) P₂ : P₃ = 4 : 9 d) P₂ : P₃ = 3 : 5. Prawidłowa odpowiedź to d, ale jak to obliczyć? 2. Podstawa trójkąta równoramiennego ma długość 16 cm, a wysokość poprowadzona na tę podstawę jest równa 6 cm. Jaką długość ma promień okręgu opisanego na tym trójkącie? 3. Z pewnego koła wycięto wycinek, którego kąt wynosi 45 stopni, a łuk tego wycinka ma długość π. Ile wynosiło pole całego koła? 4. Pole pierwszego koła jest o 36% mniejsze od pola drugiego koła. Wobec tego o ile procent promień drugiego koła jest większy od promienia pierwszego koła? Bardzo proszę o pomoc...

Aga1.: 2) Jaki jest wzór na promień okręgu opisanego na trójkącie?

Kropka: Nie ma wzoru na okrąg na trójkącie równoramiennym, a przynajmniej nigdy się o takim nie uczyłam.

Aga1.: W dowolnym trójkącie

	a*b*c
R=
	4P

a=16, b=c, bo trójkąt równoramienny i P to pole trójkąta.

Kropka: Mam to, dzięki. 2. b, c = 10 P = 48 R = {16*10*10}{4*48} R = {1600}{192} R = 8,33333333.... R ≈ 8{1}{3}

Kropka: * R= ^16*10*10_4*48 R = ¹⁶⁰⁰₁₉₂ R = 8,33333333.... R ≈ 8¹₃

Aga1.:

	1
8		jest to wartość dokładna.
	3

A dlaczego wcześniej nie skróciłaś?

Aga1.: 3) 45⁰ to jaka to część kąta pełnego?