| 1 | ||
logx | > −3 | |
| 27 |
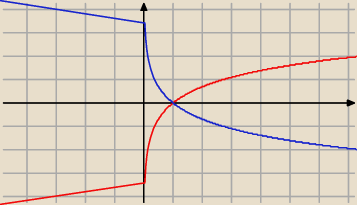 spojrz na wykres logx(c), gdzie x jest stałe.
dziedziną x jest (0;1)(1;∞)
jezeli x < 1 to funkcja ta jest malejąca (niebieski wykres)
jezeli x > 1 to funkcja jest rosnąca (czerwony wykres)
czyli dla x, ktory jest < 1, przy nierownosci trzeba zmienic znak, tzn:
logx4 < 2 (mnozenie * 1 = logxx)
logx4 < 2*logxx (wzor: clogab = loga(bc) )
logx4 < logxx2 (opuszczamy logarytmy, dla x < 1 zmieniamy znak)
4 > x2 (x tutaj jest od 0 do 1, czyli nie da sie podstawic takiej liczby, ktora bedzie wieksza
od 4)
teraz dla x > 1 (nie zmieniamy znaku − funkcja jest rosnaca)
4 < x2, tzn: x2 − 4 > 0, x ∊(−∞;−2)(2;∞), ale tutaj mamy: x > 1, wiec czescia wspolna bedzie:
x ∊ (2,∞)
P.S wykresy zle sie rysuja, nie patrz na to co jest dla x < 0
spojrz na wykres logx(c), gdzie x jest stałe.
dziedziną x jest (0;1)(1;∞)
jezeli x < 1 to funkcja ta jest malejąca (niebieski wykres)
jezeli x > 1 to funkcja jest rosnąca (czerwony wykres)
czyli dla x, ktory jest < 1, przy nierownosci trzeba zmienic znak, tzn:
logx4 < 2 (mnozenie * 1 = logxx)
logx4 < 2*logxx (wzor: clogab = loga(bc) )
logx4 < logxx2 (opuszczamy logarytmy, dla x < 1 zmieniamy znak)
4 > x2 (x tutaj jest od 0 do 1, czyli nie da sie podstawic takiej liczby, ktora bedzie wieksza
od 4)
teraz dla x > 1 (nie zmieniamy znaku − funkcja jest rosnaca)
4 < x2, tzn: x2 − 4 > 0, x ∊(−∞;−2)(2;∞), ale tutaj mamy: x > 1, wiec czescia wspolna bedzie:
x ∊ (2,∞)
P.S wykresy zle sie rysuja, nie patrz na to co jest dla x < 0 
 zmienilem znak, a zapomnialem, ze go zmienilem, oczywiscie:
0;1
wiec odpowiedz to:
x ∊(0,1)(2,∞)
zmienilem znak, a zapomnialem, ze go zmienilem, oczywiscie:
0;1
wiec odpowiedz to:
x ∊(0,1)(2,∞)
