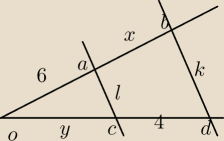
Zadania z Trygonometrii PsychoL: Znajdź dla jakiej wartości parametru m, prsote k i l są równoległe Dla jakiej wartości parametru m proste k i l są równoległe ? Mam podane że [AB]<[OA] i [CD]<[OC] x= 2m+4 y= −2m+7

Janek191:

6		x
	=
y		4

czyli

6		2m + 4
	=
− 2m + 7		4

( − 2 m + 7)*( 2 m + 4) = 6*4 − 4 m² − 8 m + 14 m + 28 = 24 4 m² − 6 m − 14 = 0 / : 2 2 m² − 3 m − 7 = 0 Δ = 9 − 4*2*(−7) = 9 + 56 = 65 √Δ = √65

	3 − √65		3 + √65
m =		lub m =
	4		4

więc

	3 − √65
x = 2 m + 4 =		+ 4 ≈ 1,47 < 6
	2

lub

	3 + √65
x = 2 m + 4 =		+ 4 ≈ 9,5 > 6 − odpada
	2

	3 − √65
Odp. m =
	4

=====================

Eta: @ Janek 24−28 = −4

Janek191: Faktycznie − wydawało mi się, że odejmuję 14 − 28

pigor: ..., m= −¹₂

Janek191: 4 m² − 6 m − 4 = 0 / : 2 2 m² − 3 m − 2 = 0 Δ = 9 − 4*2*(−2) = 9 + 16 = 25 √Δ = 5

	3 − 5
m =		= − 0,5 lub m = 2
	4

Dla m = − 0,5 x = 2*( −0,5) + 4 = 3 y = − 2* ( −0,5) + 7 = 8 x = 3 < 6 i y = 8 > 4 Dla m = 2 x = 2*2 + 4 = 8 > 6 − odpada Odp. m = − 0,5 ================

pigor: ...., bo z warunków zadania i np. tw. Talesa : 0<x<6 i y>4 i ^x₄= ⁶_y ⇔ 0< 2m+4< 6 i −2m+7>4 i xy=24 ⇔ ⇔ −4< 2m< 2 i 2m< 3 i (2m+4)(7−2m)= 24 ⇔ ⇔ −2< m<1 i m< ³₂ i 2m²−3m−2=0 ⇔ ⇔ −2< m< 1 i (m−2)(2m+1)=0 ⇔ ⇔ m= −¹₂ . ...

Eta: https://matematykaszkolna.pl/forum/227416.html

PsychoL: Dziękuje