Prawdopodobieństwo

Prawdopodobieństwo bezendu: Eta zajrzy tutaj ! W pierwszej urnie są 2 kule białe, 3 żółte, 2 szare,a w drugiej 2 białe, 1 żółta i 4 szare. Losujemy po jednej kuli z każdej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru

14
2

12!*13*14

Ω=

=

=91

12!*2

6
2

4
2

6
2

A=

+

+

	4!56		2!34		4!56
A=		+		+
	4!*2		2!*2		4!*2

	30		12		30
A=		+		+
	2		2		2

A=15+6+15 A=36

	36
P(A)=
	91

Zgadza się ?

11 gru 20:34

bezendu: ?

11 gru 20:49

Eta:

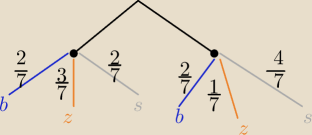
No i tu przydatne "drzewko" emotka

A= {(b,b) , (ż,ż), ( sz, sz)}

	2		2		3		1		2		4
P(A)=		*		+		*		+		*		=....
	7		7		7		7		7		7

11 gru 20:59

bezendu:

7
1

7
1

Pomyłka Ω=

*

=49

	36
P(A)=
	49

11 gru 20:59

bezendu:

4
2

4
2

6
2

A=

+

+

=27

	27
P(A)=		?
	49

11 gru 21:06

bezendu: Teraz rozpisałem dobrze a wynik nadal inny

11 gru 21:09

Eta:

	15
P(A)=
	47

11 gru 21:09

Eta:

2
1

2
1

|A|= 

*

 + ........

bo losujesz po jednej kuli z każdej urny! .......

11 gru 21:11

Eta: Jak "wleziesz " naraz do obydwu urn? emotka

11 gru 21:12

bezendu: Racja !

Dziękuję ślicznie emotka

11 gru 21:12

Eta:

11 gru 21:23

bezendu: W urnie jest 7 kul ponumerowanych od 1−7 oblicz prawdopodobieństwo, że numer drugiej kuli będzię większy od 1

7
1

6
1

Ω=

*

=42

6
1

5
1

4
1

3
1

2
1

1
1

A=

+

+

+

+

+

=21

	21
P(A)=		=0,5
	42

Mogę tak zapisać ?

11 gru 21:56

Eta: Najpierw napisz porządnie treść zadania! emotka

11 gru 21:57

bezendu: W urnie jest 7 kul ponumerowanych od 1 do 7, losujemy kolejno bez zwracania dwie kule. Oblicz prawdopodobieństwo, że numer drugiej kuli będzie większy od 1 Rozwiązanie bez zmian emotka

11 gru 21:59

bezendu: od pierwszej kuli emotka

11 gru 22:00

Saizou : ja proponuję obliczyć to przy pomocy zdarzenia przeciwnego emotka

11 gru 22:00

Saizou : to teraz zdarzenie przeciwne nie ma sensu emotka

11 gru 22:02

bezendu:

	21
Zdarzenie przeciwne P(A')=
	42

	21		21
P(A)=1−		=		=0,5
	42		42

11 gru 22:03

Saizou :

	1
bo jest tak samo prawdopodobne jak P(A)=
	2

11 gru 22:03

bezendu: A czy mój zapis 21:56 jest poprawny ?

11 gru 22:04

Saizou : ja nie widzę błędu, tylko przerost formy nad treścią

A=6+5+4+3+2+1

11 gru 22:05

Eta: |Ω|=7*6 A₁ −−− numer kuli wyciągniętej za pierwszym razem jest 1 to za drugim razem mamy 6 możliwości wyciągnięcia nr >1 A₂ −−− numer kuli za pierwszym razem jest ≠ 1 , czyli 6 możliwości to za drugim razem już tylko 5 możliwości na nr >1 ( bo bez tej pierwszej i bez jedynki |A|= |A₁|+ |A₂|=......... teraz dokończ.........

11 gru 22:06

szalik: nie

11 gru 22:07

bezendu: Moja Pani bardzo lubi drzewka, więc ja jej zrobię ''niespodziankę'' i nie będę robił drzewkiem

11 gru 22:07

bezendu: @szalik wyjdź bo nie masz chyba o tym pojęcia...

11 gru 22:08

Eta: Weź "czapkę i szalik" , bo zimno

11 gru 22:10

bezendu: emotka

11 gru 22:13

Eta:

11 gru 22:13

bezendu: Tylko jedno ?

11 gru 22:15

Saizou : bezendu zima jest trzeba oszczędzać zapasy

11 gru 22:17

Trivial: bezendu, a co, chcesz od razu całą jabłoń? emotka

11 gru 22:18

Saizou : w końcu "drzewka"

11 gru 22:19

bezendu: Trivial a czemu nie emotka

11 gru 22:19

Trivial: Proponuję zasiać. Za kilka lat może wyrośnie. emotka

11 gru 22:20

bezendu: Już rośnie właśnie emotka

11 gru 22:20

Eta: Miałam nie pomagać emotka

a tu jeszcze jabłko dostałeś

11 gru 22:23

bezendu: Czemu nie pomagać ?

11 gru 22:24