punkty A=(5,-2) i B=(17,2) sa wierzcholkami trojkata prostokatnego ABC o kacie p
kamczatka: Punkty A=(5,−2) i B=(17,2) sa wierzcholkami trojkata prostokatnego ABC o kacie prostym przy
wierzcholku A. Wierzcholek C nalezy do prostej o rownaniu y=2x+3
Oblicz pole trójkąta ABC
Wierzchołek C mam wyliczony C=(2,7)
11 gru 19:50
Hajtowy:
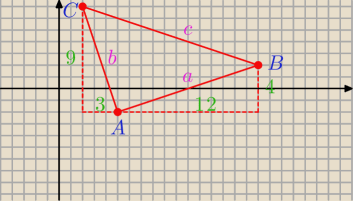
Policz z pitagorasa
A później można wykombinować coś więcej, jak to zobaczysz to powiesz
To jest moja propozycja rozwiązania
11 gru 19:54
Hajtowy:
9
2 + 3
2 = b
2 ⇒ 81+9=b
2 ⇒ 90=b
2 ⇒ b = 3
√10
12
2+4
2=a
2 ⇒ 144+16=a
2 ⇒ 160=a
2 ⇒ a = 4
√10
a
2+b
2=c
2 ⇒ (3
√10)
2 + (4
√10)
2 = c
2 ⇒ 90 + 160 = c
2 ⇒ c = 5
√10
Chyba, że źle myślę
11 gru 19:59
Piotr 10: CA→ ◯ AB→=0
[xa − xc ; ya − yc] ◯ [xb − xa ; yb − ya]=0
[5 − xc ; −2− (2xc+3)] ◯ [ 17 −5 ; 2+2]=0
(5 − xc)*12+ (−2−2xc −3)*4=0
60 − 12xc −20 −8xc=0
20xc=40
xc=2
yc=2*2+3=7
C=(2;7)
I teraz pole
11 gru 20:00
bezendu:
Piotr 10 najpierw trzeba znać wektory, a chyba Kamczatka nie zna
?
11 gru 20:01
kamczatka: bym wolał żeby to zadania zostało rozwiązane innym sposobem niż wektory.
11 gru 20:02
Piotr 10: Nie wiem czy zna, ale dla mnie najlepszy sposób
.
11 gru 20:03
bezendu: Jestem jasnowidzem
11 gru 20:03
kamczatka: a odległość AC to nie jest wysokość ?
11 gru 20:03
Piotr 10: Wektory są super
11 gru 20:04
Hajtowy: Pytanie czy kąt przy punkcie A jest prosty czy nie
11 gru 20:04
11 gru 20:06
Piotr 10: Hajtowy o dziwo ja też
11 gru 20:07