Zadania z wykorzystaniem wyrażeń wymiernych nina: Witam, mam kłopot z tym zadaniem, w pewnym momencie się zacięłam i nie wiem co dalej

	1		1		1
zad. Dana jest funkcja f(x)=		−		−		dla x≠k, x≠4, m≠0 wykaż że przy
	m2		x−k		x−4

spełnionych warunkach ta funkcja ma zawsze co najmniej 1 miejsce zerowe 1.Na początek podaną funkcję sprowadziłam do wspólnego mianownika i otrzymałam

	x2+(−4−k−m2)x +4k+4m+km2
	m2(x−4)(x−k)

2.po czym licznik przyrównałam do zera x²+(−4−k−m²)x +4k+4m²+km²=0 3.następnie postawiłam warunek że Δ≥0, po obliczeniu delty wyszło mi takie coś m⁴−24m²−6km²−24k+16≥0 I teraz powstaje problem co z tym zrobić, jakby mógł by mi ktoś pomóc to byłabym bardzo wdzięczna

nina: Jest możliwość, aby ktoś mi w tym pomógł?

Panko: W liczniku powinno być= 4k−kx−4x+x²+4m²+m²k −2xm² =x²−x(2m²+k+4) +4m²+m²k +4k

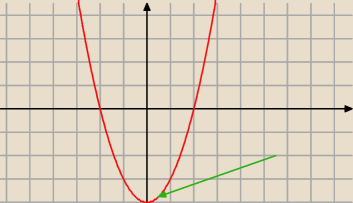
asdf: miales pochodne? − jezeli tak: funkcja kwadratowa, lim_x→∞ f(x) = ∞ wyznasz f'(x), nastepnie wykaz, ze istnieje takie ekstremum minimalne, ze funkcja w tym punkcje przyjmuje wartosci mniejsze od zera, tzn: f'(x₀) = 0 oraz f(x₀) ≤ 0 na wykresie, np. f(x) = x² − 4: f'(x₀) = 0 dla x₀ = 0 oraz f(x₀) = −4

Panko: Jeśli wykonasz kilka obrazków w wolframalpha dla różnych k to zauważysz, że g(x)= 1/(k−x) +1/(4−x) jest ściśle rosnąca ( hipoteza) w przedziale ( k, 4) lub (4,k) zależy do k. Ma tam w tym przedziale zawsze jeden pierwiastek. Więc dodanie składnika 1/m² ( dodatniego) nic zmienia dla własności funkcji g(x) jeśli idzie o posiadanie pierwiastka.