czworokąty pole równoległoboku PILNE mickeou: 1.Obwód równoległoboku jest równe 35 cm, a odległość pkt przecięcia przekątnych od dwóch sąsiednich boków równoległoboku jest odpowiednio równa 3 cm i 4 cm. Oblicz pole równoległoboku. 2.Rozpatrujemy równoległoboki, których obwód jest równy 16 cm, a kąt ostry ma miarę 45 stopni. a) wyznacz długości boków równoległoboku, którego pole jest równe 6 √2 cm² b) wyznacz długości boków równoległoboku, który ma największe pole. Oblicz to największe pole. odp. do 1. 60 cm {2} h1=6cm h2=8cm 2. a) 6cm, 2cm b) 4cm,4cm, pole 8 √2 cm²

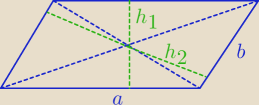
dero2005: h₁ = 6 h₂ = 8 a*h₁ = b*h₂ 2(a+b) = 35

mickeou: powiem szczerze że nie mam pojęcia jak udowodnić 2 b doszłam do tego że sinus 45 stopni odchodzi od boków jednakowych dłg ale nie wiem jak to udowodnić

Panko: 2)a) Pole równoległoboku (o bokach a, b i kacie pomiędzy nimi γ) = absinγ a+b=8 sinγ= sin45^◯= √2/2 Pole= ab√2/2 6√2= ab√2/2 ⇒12=ab ⇒12=a(8−a) ⇒a= ? (a=6) b)Pole= ab√2/2=a(a−8)√2/2 Pole(a)= √2/2* a(8−a) i a∊(0,8) Pole max osiągane jest dla a =4 jest to oczywiście x_w

tyu:

	−Δ
mam pytanie dotyczące punku 2b. W tym przypadku należy obliczyć yw =		, która się
	4a

równa bokowi a

	−b
oraz xw=		= bok b? i wtedy xw=4, yw=−4, ale yw musi być dodatnia, więc yw=4
	2a

	√2		√2
Pole największe to = 4 x 4 x		= 16		= 8√2
	2		2