funkcja kwadratowa
Tomas: Dla jakich wartości parametru m funkcja f(x)=x2 −(2m−1)x + m2 − 4 ma dwa różne miejsca zerowe
mniejsze od 4? Prosze o wytłumaczenie krok po kroku
11 gru 18:41
Kaja: funkcja ta będzie miała dwa różne miejsca zerowe, gdy Δ>0 (rozwiąż)
skoro sa one wieksze od 4, to x1>4 i x2>4. stąd x1−4>0 i x2−4>0
zatem x1−4+x2−4>0 i (x1−4)(x2−4)>0
x1+x2−8>0 i x1x2−4(x1+x2)+16>0
teraz tylko skorzystaj z wzorów Viete'a
11 gru 18:47
Eta:
11 gru 18:50
Kaja: miały być mniejsze czyli x1<4 i x2<4
(x1−4)(x2−4)>0 i x1−4+x2−4<0
11 gru 18:51
Kaja: i dalej x1x2−4(x1+x2)+16>0 i x1+x2−8<0 i skorzystaj z wzorów Viete'a
11 gru 18:52
Bizon:
1. Dwa różne miejsca zerowe ... Δ>0
(2m−2)
2−4m
2>0
2. x
w<4
| | 2m−1 | |
|
| <4 ⇒ 2m−1<8 ⇒ 2m<9 ⇒ m<4,5 |
| | 2 | |
3. f(4)>0
16−4(2m−1)+m
2−4>0
16−8m+4+m
2−4>0
m
2−8m+16>0 ⇒ (m−4)
2>0 m∊R\{4}
Ostatecznie
m<0,5
11 gru 19:02
Eta:
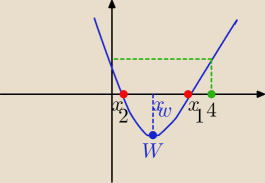
{Δ>0
{f(4) >0
{x
w<4
11 gru 19:05
Eta:
11 gru 19:06
Bizon:
... coś "nachomotałem" −:(
11 gru 19:08
Bizon:
... no tak ....w Δ
(2m−1)2−4{m2−4)>0
11 gru 19:13
Tomas: odpowiedz ma wynosić
la m ∊ (−
∞ ;4) ∪ (4;4.5) , a mi dalej tak nie wychodzi
11 gru 19:17
Bizon:
4m2−4m+1−4m2+16>0
−4m+17>0
m<17/4
... i teraz tak wychodzi
11 gru 19:25