planimetria

planimetria Radek: rysunek

Aga1 spójrz jak masz czas emotka

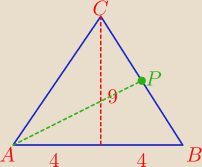
Podstawa trójkąta równoramiennego ma długość 8, a wysokość poprowadzona z wierzchołka trójkąta ma 9. Jakie długości mają środkowe tego trójkąta CB=9²−4² CB=√65

	√65		√65
Teraz wiem, że CP=		i PB =
	2		2

ale jak wyliczyć tą środkową ?

11 gru 12:14

Aga1.: Jedna ze środkowych to wysokość. Znasz twierdzenie cosinusów? Druga to IAPI IAPI²=8²+IPBI²−2*8*cosB

11 gru 12:22

Bizon: zauważ, że wysokość trójkąta równoramiennego jest również jego środkową. Dalej twierdzenie o środkowych (2:1)

11 gru 12:23

Radek: Znam, ale która środkowa jest wysokością?

11 gru 12:24

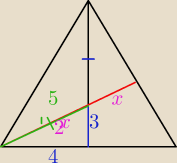
Aga1.: rysunek

Wysokość h=9 jest środkową oraz IAPI. AP=7,5 można obliczyć też z twierdzenia Pitagorasa , wykorzystując wspomniane własności środkowych.

11 gru 12:31

Radek: A czemu AD nie może być wysokością ? Patrząc na mój rysunek

11 gru 15:23

Bizon: chyba pytasz o AP .... bo nie widzę D

11 gru 15:25

Radek: Punkt D leży na połowie Boku AB teraz już widzisz emotka

11 gru 15:28

Bizon: ... to ta wysokość jest jednocześnie środkową Pozostałe wysokości nie są jednocześnie środkowymi

11 gru 15:30

Radek: Ok dzięki Bizon emotka

11 gru 15:33

Bizon: − emotka

11 gru 15:34