Równanie kwadratowe z parametrem Tom: Dla jakich wartości parametru m równanie |x² −2mx| = 1 ma trzy pierwiastki

Aga1.: Ix²−2mxI=1 x²−2mx=1 lub x²−2mx=−1 Pierwsze równanie ma 1 pierwiastek i drugie 2 pierwiastki lub na odwrót .

Tom: Mogłabyś to rozpisać, bo nie do końca rozumiem...?

Bizon: a może tak: |x²−2mx|=1

	1
|x|*|x−2m|=1 ⇒ |x−2m|=|		| itd −
	x

Tom: Aga1 Δ>0 ⇒ 4m² + 4 > 0 Δ=0 ⇒ 4m² − 4 = 0 W ten sposób?

Bizon: 4m2 + 4 > 0 jak widzisz .to zachodzi dla dowolnego m zatem?

Tom: Zatem m∊R − brak miejsc zerowych, bo parabola skierowana do góry

zombi: y=|x(x−2m)| Wiemy, że parabola ma jedno miejsce zerowe x₁=0 i ramiona skierowane do góry, wobec tego jak przetniemy je na wysokości y=1 dostaniemy 2 rozwiązania, trzecia rozwiązanie jedyne możemy otrzymać jeśli nasza funkcja y=|x(x−2m)| odbije wierzchołek na 1, zatem funkcja pierwtona x(x−2m) musi mieć wierzchołek q=−1. i tyle.

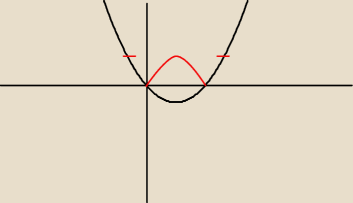
zombi: To jest jeden z przypadków, żeby zobrazować jak to ma wyglądać.