planimetria
Radek:
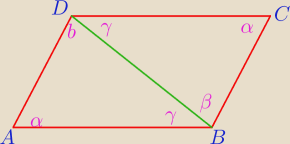
Wykaż, że przekątna równoległoboku dzieli równoległobok na dwa trójkąty przystające
kbk ?
10 gru 20:01
matyk: Dokładnie tak.
10 gru 20:04
Radek:
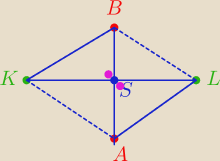
odcinki AB i KL przecinają się w punkcie S będącym środkiem obu odcinków, wykaż, że ΔLAS i ΔKBS
są przystające
Te trójkąty mają kąt wierzchołkowy ale co dalej ?
10 gru 20:14
matyk: "będącym środkiem obu odcinków"
10 gru 20:17
matyk: Podobieństwo ze skalą 1= przystawanie
10 gru 20:17
MQ: Po co tak kombinujecie? Przecież to wychodzi natychmiast: bok−bok−bok.
10 gru 20:33
Radek:
Czyli jak ?
10 gru 20:34
matyk: Ja widzę b−k−b
10 gru 20:41
Radek:
Ja też
10 gru 20:42
MQ:
Z definicji równoległoboku: AB=CD oraz AD=CB
Dodatkowo mamy: DB=DB
Na mocy I cechy przystawania trójkątów, trójkąty BAD i DCB są przystające.
10 gru 20:45