u. rownan
Leki: Miejscowości A,B oraz C leża przy tej samej drodzę, przy czym, miejscowość B lezy pomiedzy A i
C. Z miejscowości A i B, odległych o 36 km, wyruszają jednocześnie rowerzyści. każdy z nich
jedzie ze stałą prędkością. Gdyby obaj jechali naprzeciw siebie to spotkaliby się po 1 i 1/8 h
. Gdyby obaj jechali w kierunku miejscowości C , to po 5 h jazdy odleglość między nimi
wynosiłaby 24 km. Z jaką predkoscią jedzie każdy rowerzysta?
10 gru 19:42
Leki: Pomoże ktoś ? Proszę
10 gru 20:08
Leki: ?
10 gru 20:14
pigor: .... wychodzi mi
x=[n[19,6 km/h] i y=[n[12,4\\ km/h − stałe prędkości rowerzysty z A i B odpowiednio,
a co masz w odpowiedziach

10 gru 20:36
pigor: ... , kurcze, jeszcze raz 19,6 km/h i 12,4 km/h odpowiednio z A i B.
10 gru 20:38
koma: x=22km/h y=10km/h
lub x=17,2km/h y=14,8km/h
10 gru 20:41
koma: ma ktoś jakiś pomysł?
10 gru 20:44
matyk:
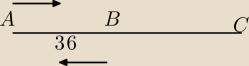
Jadąc w "swoją" stronę szybkość względna to różnica ich szybkości.
10 gru 20:49
koma: W pierwszym przypadku:
36=(V1+V2)* 9/8
ale nie wiem jak drugi
10 gru 20:50
pigor: ... ,

no jasne, to już wiem, więc niech
x,y=? −szukane prędkości
z miejscowości A i B odpowiednio, to z warunków zadania mam np. taki
układ równań
98x= −98y+36 /*89 i (5y+36−5x= 24 lub 5x−5y−36=24) ⇔
⇔ (x= −y+32 /*5 i 5y−5x= −12) lub (x= −y+32 i 5x−5y= 60) ⇔
⇔ (5x+5y= 160 i −5x+5y= −12) lub (5x+5y= 160 i 5x−5y= 60) /±stronami ⇔
⇔ (10y= 148 i 10x= 172) lub (10x= 220 i 10y= 100) / : 10 ⇔
⇔ (x , y)= (
17.2 km/h , 14.8 km/h) lub (x , y)= ([c[22 km/h , 10km/h. ...

10 gru 21:05
10 gru 21:50

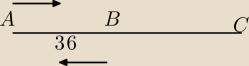 Jadąc w "swoją" stronę szybkość względna to różnica ich szybkości.
Jadąc w "swoją" stronę szybkość względna to różnica ich szybkości.
 no jasne, to już wiem, więc niech x,y=? −szukane prędkości
z miejscowości A i B odpowiednio, to z warunków zadania mam np. taki
układ równań
98x= −98y+36 /*89 i (5y+36−5x= 24 lub 5x−5y−36=24) ⇔
⇔ (x= −y+32 /*5 i 5y−5x= −12) lub (x= −y+32 i 5x−5y= 60) ⇔
⇔ (5x+5y= 160 i −5x+5y= −12) lub (5x+5y= 160 i 5x−5y= 60) /±stronami ⇔
⇔ (10y= 148 i 10x= 172) lub (10x= 220 i 10y= 100) / : 10 ⇔
⇔ (x , y)= (17.2 km/h , 14.8 km/h) lub (x , y)= ([c[22 km/h , 10km/h. ...
no jasne, to już wiem, więc niech x,y=? −szukane prędkości
z miejscowości A i B odpowiednio, to z warunków zadania mam np. taki
układ równań
98x= −98y+36 /*89 i (5y+36−5x= 24 lub 5x−5y−36=24) ⇔
⇔ (x= −y+32 /*5 i 5y−5x= −12) lub (x= −y+32 i 5x−5y= 60) ⇔
⇔ (5x+5y= 160 i −5x+5y= −12) lub (5x+5y= 160 i 5x−5y= 60) /±stronami ⇔
⇔ (10y= 148 i 10x= 172) lub (10x= 220 i 10y= 100) / : 10 ⇔
⇔ (x , y)= (17.2 km/h , 14.8 km/h) lub (x , y)= ([c[22 km/h , 10km/h. ... 