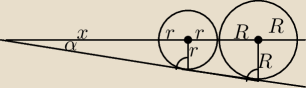
Gdzie jest bląd? tyu: Okrąg o środku A i promieniu długości r jest styczny zewnętrznie do okręgu o środku B i promieniu długości R (R> r). Prosta k jest styczna jednocześnie do obu okręgów i tworzy z prostą AB kąt ostry a. Wyznacz sina w zależności od r i R. Oto moje rozwiązanie (co jest w nim źle?)

	r
sinα=
	r+x

	R
sinα=
	R+2r+x

R		r
	=
R+2r+x		r+x

	−2r2
x=
	r−R

	r
sinα=
	−2r2   r+   r−R

zefiryna: W przekształceniach. Prawidłowo ( po rozwiazaniu proporcji ) winno być x BEZ MINUSA, co daje wynik na kąt α = arcsin((R−r)/(R+r))... Zresztą to rozwiązanie jest "zbyt drogie" z ekonomicznego punktu widzenia: wystarczy bowiem narysowac trapez prostokątny wyznaczony przez środki okregów i punkty styczności, odjąć od siebie boki o długości R i r : mamy gotowy trójkącik o hipotenuzie równej R+r...

tyu: przy x nie ma minusa R>r

tyu: up!

tyu: ?

zefiryna: Po prawej stronie bez minusa...

tyu: chodzi mi o to ze x będzie >0

MQ: Przede wszystkim:

r
	=tgα, a nie sinα
r+x

Tak samo z drugim równaniem.

MQ: Nie, cofam, jest OK −− zmylił mnie twój rysunek.

elsaper: a może sprowadz mianownik do wspólnego mianownika i poskracaj?