Funkcja kwadratowa, moduły w module, pierwiastki, parametry
Ojaz: Witam serdecznie. Otóż po raz pierwszy tak długo borykam się z przyswojeniem sobie materiału z
matematyki i proszę was o pomoc w rozwiązaniu kilku zadań a wiem, że część osób rozwiąże je z
przyjemnością

. Byłoby mi również dużo prościej, gdyby czasem pojawił się jakiś komentarz,
czemu właśnie tak się postępuje i jakieś zwizualizowanie tej funkcji kwadratowej, gdyż same te
liczby kompletnie mi nic nie mówią.
| | f(1) | |
1. Korzystając z postaci iloczynowej funkcji kwadratowej f(x), wyznacz |
| , jeśli |
| | f(−1) | |
wiesz, że pierwiastkami tej funkcji są 5 i 7.
2. Naszkicuj wykres funkcji f(x) = x
2 + 2|x| − 3. Podaj jej zbiór wartości. dla jakich
wartości parametru m równanie f(x) = m ma dwa rozwiązania?
3. Dla jakich wartości parametru m dziedziną funkcji f(x) =
√x2 − 4x + 5m jest zbiór liczb
rzeczywistych?
4. Rozwiąż równanie |x
2 − |x| − 2| = 2.
To co prawda nie wszystkie z którymi się trudzę, ale co za dużo to niezdrowo, więc na początek
tyle

.
9 gru 21:48
PW: Zadanie 1. Skoro funkcja kwadratowa f ma pierwiastki 5 i 7, to jej postać iloczynowa wygląda
następująco:
f(x) = a(x−5)(x−7), a≠0.
Wobec tego
| | f(1) | | a(1−5)(1−7) | |
|
| = |
| = ... |
| | f(−1) | | a(−1−5)(−1−7) | |
Współczynnik „a” w liczniku i w mianowniku skróci się, a w rachunkach przeważnie się mylę, więc
od razu zrób to sam.
9 gru 22:02
Aga1.: 4.
Ix2−IxI−2I=2
x2−IxI−2=2 lub x2−IxI−2=−2
x2−IxI−4=0
Rozpatrz 2 przypadki
x≥0
x2−x−4=0
lub x<0
x2+x−4=0
9 gru 22:14
pigor: ..., 4. Rozwiąż równanie
|x2−|x|−2|= 2 .
cóż, ja widzę rozwiązanie w swojej ...

szufladzie
np. tak :
|x2−|x|−2|=2 ⇔ |x|
2−|x|−2= −2 v |x|
2−|x|−2=2 ⇔
⇔ |x|
2−|x|=0 v |x|
2−|x|=4 ⇔ |x|(|x|−1)=0 v |x|
2−2*
12|x|+
14=4+
14 ⇔
⇔ x=0 v |x|=1 v (|x|−
12)
2=
14*17 ⇔
x∊{0,−1,1} v
v |x−
12|=
12√17 ⇔
x∊{−1,0,1, 12(1−√17), 12(1+√17)} .

9 gru 22:21
bezendu:
pigor Twoja szuflada nie ma dna ?

9 gru 22:22
PW: pigor, też piszesz książkę (zbiór zadań z rozwiązaniami)? Podziwiam Twoje skondensowane
podejście typu "⇔".
9 gru 22:33
Ojaz: Powiedzcie mi jak z tego |x|2−|x|=4 przejść do tego |x|
2−2*
12|x|+
14=4+
14 bo
jest to dla mnie czarna magia aktualnie (chyba że to kwestia pory dnia).
Dodatkowo czemu moduł w 4 zadaniu na samym początku znika z całości i zostaje tylko na |x|
2 ?
| | 1 | |
Co do zadania 1. to po prostu wychodzi |
| ? Na prawdę? Aż żal patrzeć że to takie proste |
| | 2 | |
jest a ja tego nie potrafię...
10 gru 00:20
pigor: ..., przepraszam, ale ja jestem już taki ...

chomik ,
Ojaz , a co do mojego przejścia, to jak nie czujesz tego, to
możesz pobawić się deltą i policzyć sobie te brzydkie pierwiastki ;
co do znikania modułu to wynika to z jego definicji
|a|=b ⇔ a= −b v a=b i tyle . ...

−−−−−−−−−−−−−−−−−−−−−
10 gru 00:35
pigor: ... 2. Naszkicuj wykres funkcji
f(x)= x2+2|x|−3. Podaj
jej zbiór wartości. Dla jakich wartości parametru m równanie
f(x)= m ma dwa rozwiązania ?
−−−−−−−−−−−−−−−−−−−−−−−−
otóż np. tak :
f(x)= x2+2|x|−3= |x|
2+2|x|+1−4=
(|x|+1)2−4 , a więc
f(0)=1−4= −3 f(1)=f(−1)=0 itp. − z parzystości funkcji f, czyli jej wykres
jest symetryczny względem OY, zbiór wartości
ZWf.= [−3;+∞) , a równanie
f(x)=m ma
2 rozwiązania ⇔
m >3 ⇔
m∊(3;+∞) i to tyle .

10 gru 01:52
Aga1.:
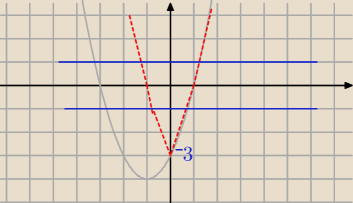
A wykres wygląda tak
Narysowałam h(x)=x
2+2x−3 kolor szary , a później
f(x)=h(IxI)=IxI
2+2IxI−3=x
2+2IxI−3 kolor czerwony
A f(x)=m ma 2 rozwiązania dla m>
−3
10 gru 08:39
pigor: przepraszam, no jasne to są skutki nocnego "czuwania"
bo napisałem
ZWf.= [−3;+∞) , a co potem to chyba nie ja o 1:52 w nocy

10 gru 14:10
 . Byłoby mi również dużo prościej, gdyby czasem pojawił się jakiś komentarz,
czemu właśnie tak się postępuje i jakieś zwizualizowanie tej funkcji kwadratowej, gdyż same te
liczby kompletnie mi nic nie mówią.
. Byłoby mi również dużo prościej, gdyby czasem pojawił się jakiś komentarz,
czemu właśnie tak się postępuje i jakieś zwizualizowanie tej funkcji kwadratowej, gdyż same te
liczby kompletnie mi nic nie mówią.
 .
.
 szufladzie
np. tak :
|x2−|x|−2|=2 ⇔ |x|2−|x|−2= −2 v |x|2−|x|−2=2 ⇔
⇔ |x|2−|x|=0 v |x|2−|x|=4 ⇔ |x|(|x|−1)=0 v |x|2−2*12|x|+14=4+14 ⇔
⇔ x=0 v |x|=1 v (|x|−12)2= 14*17 ⇔ x∊{0,−1,1} v
v |x−12|=12√17 ⇔ x∊{−1,0,1, 12(1−√17), 12(1+√17)} .
szufladzie
np. tak :
|x2−|x|−2|=2 ⇔ |x|2−|x|−2= −2 v |x|2−|x|−2=2 ⇔
⇔ |x|2−|x|=0 v |x|2−|x|=4 ⇔ |x|(|x|−1)=0 v |x|2−2*12|x|+14=4+14 ⇔
⇔ x=0 v |x|=1 v (|x|−12)2= 14*17 ⇔ x∊{0,−1,1} v
v |x−12|=12√17 ⇔ x∊{−1,0,1, 12(1−√17), 12(1+√17)} . 

 chomik ,
Ojaz , a co do mojego przejścia, to jak nie czujesz tego, to
możesz pobawić się deltą i policzyć sobie te brzydkie pierwiastki ;
co do znikania modułu to wynika to z jego definicji
|a|=b ⇔ a= −b v a=b i tyle . ...
chomik ,
Ojaz , a co do mojego przejścia, to jak nie czujesz tego, to
możesz pobawić się deltą i policzyć sobie te brzydkie pierwiastki ;
co do znikania modułu to wynika to z jego definicji
|a|=b ⇔ a= −b v a=b i tyle . ...  −−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−−−−−−−−−−−

 A wykres wygląda tak
Narysowałam h(x)=x2+2x−3 kolor szary , a później
f(x)=h(IxI)=IxI2+2IxI−3=x2+2IxI−3 kolor czerwony
A f(x)=m ma 2 rozwiązania dla m>−3
A wykres wygląda tak
Narysowałam h(x)=x2+2x−3 kolor szary , a później
f(x)=h(IxI)=IxI2+2IxI−3=x2+2IxI−3 kolor czerwony
A f(x)=m ma 2 rozwiązania dla m>−3
