Dwa zadania tekstowe Thaid: 1. W pewnym prostokącie jeden z boków skrócono, a drugi wydłużono o p% tak, że w rezultacie pole prostokąta zmniejszyło się o 9%. Oblicz p. 2.W kostce sześciennej przeprowadzono płaszczyznę przechodzącą przez przekątne 3 sąsiednich ścian. Objętość odciętej mniejszej części sześcianu wynosi 36m². Oblicz długość krawędzi sześcianu.

Thaid: Nikt się nie skusi ?

Tripos: 1. a*b = P (a − ^p₁₀₀) * (b+^p₁₀₀) = 0,91 P Dalej sam dasz rady

Eta: 1/ (1−p)(1+p)ab= 0,91ab ⇒ 1−p²= 0,91 ⇒ p²= 0,09 ⇒ p=0,3= 30%

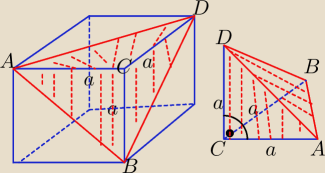
Eta: V odciętego naroża , jego podstawą jest połówka kwadratu o boku "a" , i wysokością "a" naroże jest ostrosłupem

	1		1		1
V( ostrosłupa CABD)=		*		a2*a=		a3
	3		2		6

1
	a3= 36 ⇒ a3= .... ⇒ a= ....
6

Thaid: Dziękuje