udowodnij z geometrii
Janek:
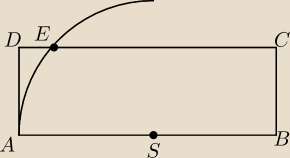
W prostokącie ABCD punkt S jest środkiem boku AB, |AB|>2|BC|. Poprowadzono łuk okręgu o środku
w punkcie S i promieniu |AS|, który przeciął bok DC w punkcie E. Wykaż, że kwadrat o boku AD
ma takie samo pole jak prostokąt, którego boki mają długość |DE| i |EC|.
9 gru 18:26
Enee: Wiem tylko że trojkat AED jest podobny do trójkąta EBC
AD:EC= ED:BC
....a resztę ktos napisze?
16 gru 16:22
16 gru 16:26
Panko: Przecież dawno już zamieściłem rozwiązanie.
Post o tym był kilka dni temu
Wystarczy tylko zastosować TW o odcinkach prostej siecznej i stycznej do okręgu
poprowadzonych z jednego punktu
16 gru 17:37
Enee: Dziękuje bardzoo
16 gru 19:25