zadanie prowadzacące do równania kwadratowego mateusz: W trójkącie prostokątnym ABC kąt przy wierzchołku C jest prosty. Wysokość CD dzieli przeciwprostokątną AB na odcinki AD i DB tak, że |DB|=3|AD|+2. Wiedząc dodatkowo, że |CD|=|AD|+2, oblicz pole trójkąta ABC oraz promień koła wpisanego w ten trójkąt.

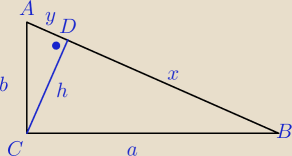
Janek191: I DB I = 3*I AD I + 2 I CD I = I AD I + 2 czyli x = 3 y + 2 h = y + 2 Mamy h² = x*y ( y + 2)² = ( 3 y + 2)*y y² + 4 y + 4 = 3 y² + 2 y 2 y² − 2 y − 4 = 0 / : 2 y² − y − 2 = 0 ( y − 2)*( y + 1) = 0 y = 2 lub y = − 1 − odpada, bo y −długość odcinka ==== x = 3*2 + 2 = 8 c = I AB I = x + y = 8 + 2 = 10 h² = x*y = 8*2 = 16 h = 4 zatem P_ΔABC = 0,5 I AB I *h = 0,5 *10*4 = 20 [ j² ] ============================================ b² = h² + y² = 4² + 2² = 16 + 4 = 20 = 4*5 b = 2 √5 ======== a² = x² + h² = 8² + 4² = 64 + 16 = 80 = 16*5 a = 4 √5 ======== Obwód L = a + b + c = 4 √5 + 2 √5 + 10 = 6√5 + 10

	2 P
P = 0,5 L*r ⇒ r =
	L

r − promień koła wpisanego w ten trójkąt

	40		20
r =		=		= 3 √5 − 5 ≈ 1,7
	6√5 + 10		3 √5 + 5

====================================