 b) (x2−6x+8)(x−2)(x+2)(x−7)≥0
zatem (x2−6x+8)=0 ⋁(x−2)=0 ⋁ (x+2)=0 ⋁(x−7)=0
(x2−6x+8)=0⇒ Δ=36−32=4 zatem x1=2 , x2=4;
(x−2)=0 (x+2)=0 (x−7)=0
x=2 x=−2 x=7
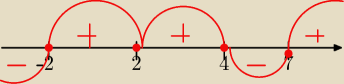
mamy nastepujące pierwsiaski:−2, 2 (podwójny), 4 i 7 . zaznaczamy pierwsiatki to na osi
liczbowej.
poniewż ma być większe bądź równe 0 a wieć rozwiązaniem jest: x∊<−2,2>∪<7,+∞).
b) (x2−6x+8)(x−2)(x+2)(x−7)≥0
zatem (x2−6x+8)=0 ⋁(x−2)=0 ⋁ (x+2)=0 ⋁(x−7)=0
(x2−6x+8)=0⇒ Δ=36−32=4 zatem x1=2 , x2=4;
(x−2)=0 (x+2)=0 (x−7)=0
x=2 x=−2 x=7
mamy nastepujące pierwsiaski:−2, 2 (podwójny), 4 i 7 . zaznaczamy pierwsiatki to na osi
liczbowej.
poniewż ma być większe bądź równe 0 a wieć rozwiązaniem jest: x∊<−2,2>∪<7,+∞).
