f. kwadratowa Iza: dla jakich wartosci parametru a suma kwadratow pierwiastkow rownania x³ +ax −a+3=0 osiaga najmniejszą wartość? wiem że delta większa od zera, i wychodzi z tego ze a ∊ (−∞,−6> suma <2,∞) drugi warunek to x1²+x2²=min i z wzorów vieta rowniez to wyliczylam, wychodzi mi funkcja f(a)=a² +2a−6 ktoś mi może powiedziec co mam teraz zrobic? parabola jest skierowana ramionami do góry, mam liczyć p? czemu nie q? pomocy!

Okła: nie mozesz tak zrobic z vieta. najpierw musisz rozpisac, bo nie mamy wzoru na x₁²+x₂² tylko x₁+x₂. Więc. x₁²+x₂²= (x₁+x₂)² −2*x₁*x₂

Okła: śmiem rozumieć, że tam jest x² nie do ³ Musisz teraz obliczyć p dlatego ze pytają się dla jakiej wartości. trzeba obliczyć p z wykresu f(a) p=−b/2a=−2/2=−1 dla wartośći −1 suma kwadratów osiąga najmniejsząwartość P.S. sorry, nie zauważyłem, że tak zrobiłaś.

pigor: ..., jesli twoja funkcja f jest dobra, to możesz dalej np. tak : f(x)=a²+2a−6= a²+2a+1−7= (a+1)²−7 ⇒ a=1 − szukana wartość a i f(−1)= −7= f_min

pigor: ..., oczywiście "zjadłem" znak minus , a więc a=−1

suchy: ale a=−1 nie należy do zbioru wynikającego z delty. Podstawiając pod główny wzór funkcji x² + (−1)x −(−1)+3=0 x² −x + 4 =0 delta wychodzi ujemna, więc nie ma ona dwóch rozwiązań które których suma kwadratów miała osiąfać najmniejszą wartość ... prosze o pomoc

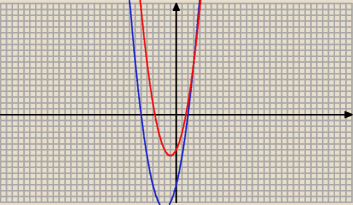
Janek191: x² + a x − a + 3 = 0 Δ = a² − 4*1*( − a + 3) = a² + 4a − 12 > 0 ⇔ ( a + 6)*( a − 2) > 0 ⇔ a < − 6 ∨ a > 2 x₁² + x₂² = ( x₁ + x₂)² − 2 x₁*x₂ = ( −a)² − 2*( −a + 3) = a² + 2a − 6 f(a) = a² + 2a − 6 Wykresy : Δ ( a) = a² + 4a − 12 − niebieska parabola f(a) = a² + 2a − 6 − czerwona parabola

	−2
Funkcja f osiągnęłaby najmniejszą wartość dla a = p =		= −1, ale dla a = −1
	2

Δ < 0 i nie ma dwóch pierwiastków. Nie ma takiej wartości a =================== Może w treści zadania jest pomyłka ?

Ola: dla wartości a=2 suma kwadratów x₁² + x₂² osiąga najmniejszą wartość równą 2