Planimetria
Radek:
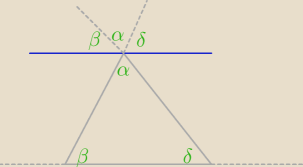
Przez jeden bok z wierzchołka trójkąta poprowadzono prostą równoległą do przeciwległego boku,
udowodnij, że miara kątów w trójkącie 180
0
α+β+δ=180
0 takie coś wystarczy ?
8 gru 13:27
Radek:
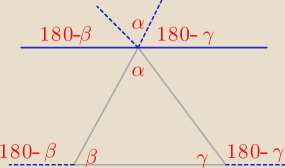
chyba jednak coś nie tak

8 gru 13:37
Kaja: skorzystaj z tego że kąty naprzemianległe przy prostych równoległych są takie same
8 gru 13:44
Radek:
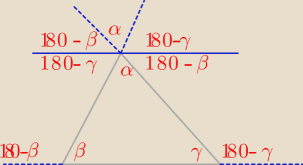
α+α+180−β+180−β+180−γ+180−γ=360
2α−2β+2γ=−180/ : (−2)
−α+β+γ=90
−α=90−β−γ
α=β+γ−90
8 gru 13:51
Kaja: Radek chyba widać gołym okiem że ten jeden kąt 180−β na dole nie jest równy temu na górze.
zamiast 180−β (tam po prawej stronie) daj γze względu że ten kąt i γ w trójącie to
naprzemianległe. tak samo z β (tam gdzie masz 180−γ po lewej jest β). i wtedy masz β+α+γ=180o
8 gru 13:55
Radek: a to nie są katy odpowiadające ?
8 gru 13:58
Kaja: nie.
8 gru 14:00
8 gru 14:02
Kaja: u ciebie kąty odpowiadające to 180−β i 180−β+α
8 gru 14:07
Radek:
A no tak racja, przepraszam

8 gru 14:09
Radek:
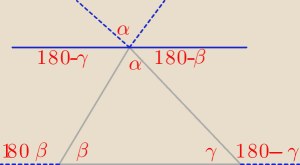
α+180−β+180−γ=180
α−β−γ=−180
−α+β+γ=180
β+γ=180+α
a dalej ?
8 gru 14:17
Radek: ?
8 gru 14:22
Kaja: to 180−γ i 180−β u góry pod prostą też nie jest dobrze. tam gdzi masz 180−β wpisz γ, a tam gdzi
180−γ wpisz β
8 gru 14:25
Radek:
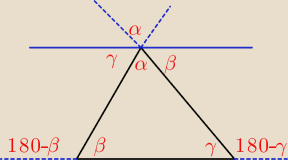
α+β+γ=180
8 gru 14:28
Kaja: γ i β na odwrót
8 gru 14:30
Kaja: dobrze ci napisałam wczesniej jak ma być
8 gru 14:30
Radek:
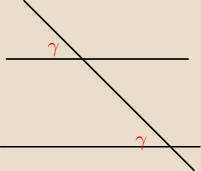
to nie są kąty naprzemianległe bo leżą po jednej stronie prostej ?
8 gru 14:31
Kaja: te są odpowiadające
8 gru 14:31
Radek:
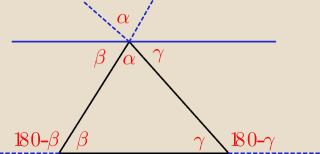
8 gru 14:33
Kaja: tak
8 gru 14:34
Radek: i koniec zadania?
8 gru 14:35
 Przez jeden bok z wierzchołka trójkąta poprowadzono prostą równoległą do przeciwległego boku,
udowodnij, że miara kątów w trójkącie 1800
α+β+δ=1800 takie coś wystarczy ?
Przez jeden bok z wierzchołka trójkąta poprowadzono prostą równoległą do przeciwległego boku,
udowodnij, że miara kątów w trójkącie 1800
α+β+δ=1800 takie coś wystarczy ?
 chyba jednak coś nie tak
chyba jednak coś nie tak 
 α+α+180−β+180−β+180−γ+180−γ=360
2α−2β+2γ=−180/ : (−2)
−α+β+γ=90
−α=90−β−γ
α=β+γ−90
α+α+180−β+180−β+180−γ+180−γ=360
2α−2β+2γ=−180/ : (−2)
−α+β+γ=90
−α=90−β−γ
α=β+γ−90
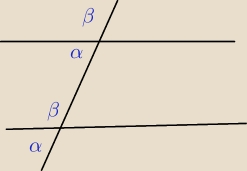 https://matematykaszkolna.pl/strona/3012.html
czemu niby nie są odpowiadające ?
https://matematykaszkolna.pl/strona/3012.html
czemu niby nie są odpowiadające ?

 α+180−β+180−γ=180
α−β−γ=−180
−α+β+γ=180
β+γ=180+α
a dalej ?
α+180−β+180−γ=180
α−β−γ=−180
−α+β+γ=180
β+γ=180+α
a dalej ?
 α+β+γ=180
α+β+γ=180
 to nie są kąty naprzemianległe bo leżą po jednej stronie prostej ?
to nie są kąty naprzemianległe bo leżą po jednej stronie prostej ?
