Zadanie maturalne
Radek:
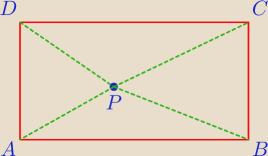
Punkt P leży wewnątrz prostokąta ABCD. Wykaż, że suma pól trójkątów APD i BPC jest równa sumie
pól trójkątów APB i DPC
ΔAPD+ΔBDC=ΔAPB+ΔDPC
L=|AP|+|DP|>|AD|
|BP|+|CP|>|CB|
L=|AP|+|DP|+|BP|+|CP|>|AD|+|CB|
P=|AP|+|BP|>|AB|
|DP|+|CP|>|CD|
P=|AP|+|BP|+|DP|+|CP|>|AB|+|DC|
OK ?
7 gru 23:02
MQ: Nie OK. Przecież to nic nie ma do pól.
7 gru 23:05
Radek:
Czyli z czego mam skorzystać ?
7 gru 23:06
MQ: Narysuj wysokości tych trójkątów, to ci się rozjaśni.
7 gru 23:07
Radek:
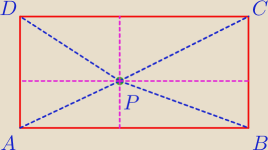
7 gru 23:10
MQ: Szkoda, że ich nie oznaczyłeś, bo było by mi łatwiej.
Zauważ, że suma poziomych wysokości jest równa AB, więc suma "poziomych trójkątów jest 1/2 pola
prostokątu.
Z pionowymi jest tak samo.
7 gru 23:13
MQ: Można też z przystawania trójkątów −− bardziej zgrabne.
7 gru 23:14
Radek: Dzięki, już wiem jak dokończyć

7 gru 23:19
 Punkt P leży wewnątrz prostokąta ABCD. Wykaż, że suma pól trójkątów APD i BPC jest równa sumie
pól trójkątów APB i DPC
ΔAPD+ΔBDC=ΔAPB+ΔDPC
L=|AP|+|DP|>|AD|
|BP|+|CP|>|CB|
L=|AP|+|DP|+|BP|+|CP|>|AD|+|CB|
P=|AP|+|BP|>|AB|
|DP|+|CP|>|CD|
P=|AP|+|BP|+|DP|+|CP|>|AB|+|DC|
OK ?
Punkt P leży wewnątrz prostokąta ABCD. Wykaż, że suma pól trójkątów APD i BPC jest równa sumie
pól trójkątów APB i DPC
ΔAPD+ΔBDC=ΔAPB+ΔDPC
L=|AP|+|DP|>|AD|
|BP|+|CP|>|CB|
L=|AP|+|DP|+|BP|+|CP|>|AD|+|CB|
P=|AP|+|BP|>|AB|
|DP|+|CP|>|CD|
P=|AP|+|BP|+|DP|+|CP|>|AB|+|DC|
OK ?

