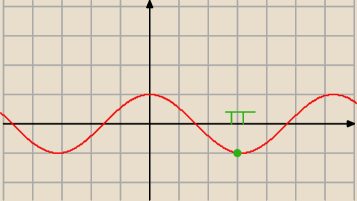
równanie Radek: Równania trygonometryczne−problem mam takie równanie cosx=−1 x=π+2kπ więc powinno być jeszcze x=−π+2kπ

Radek: ?

Radek: ?

5-latek: https://matematykaszkolna.pl/strona/1586.html

Radek: Fajnie, tylko nic z tego nie kumam, wykres to sobie narysowałem

Radek: Może ktoś mi pomóc ? Bo już nie wiem ile ''?'' dziś napisałem...

MQ: −π=π−2π=π+2*(−1)*π ⇒ k=−1 Nie ma potrzeby więc rozbijać na π i −π, bo w tym wypadku k i k' różnią się o −1

Alfa: kąty π i −π różnią się o 2π, czyli okres cosinusa, więc z obu tych odp. otrzymasz te same kąty. Zatem wystarczy podać tylko jedną z nich − zwykle podaje się odp. z kątem dodatnim (czyli pierwszą), ale można odpowiedzieć w ten drugi sposób i też będzie dobrze.

Radek: Dzięki.

Eta: cosx= a , a∊<−1,1> x_o −−− rozwiązanie szczegółowe x= x_o +2kπ v x= −x_o +2kπ cosx= −1 , x_o= π x= π+2kπ v x= −π +2kπ x = 2π −π+2kπ x= π+2kπ zatem x= π+2kπ , k∊C sinx= a , a∊<−1,1> x= x_o +2kπ v x= π−x_o+2kπ tgx=a , a∊R x= x_o+k*π , podobnie ctgx= a

Radek: a to równanie

	1
cosx=−
	2

	π		π
x=−		+2kπ lub x=		+2kπ
	3		3

?

Eta:

Radek: ale nie rozumiem jednego przejścia czemu w cosx=−1 x₀=π ok x=π+2kπ ok x=−π+2kπ ok x=2π−π+2kπ ?

Radek: ?

Radek: ?

Eta: No zamieniasz miarę ujemną na dodatnią −π= 2π−π= π

Radek: a nie może zostać ujemna ?

Eta: Może zostać ale bardziej elegancko ...zapisać dodatnią miarę tego kąta

Radek: a sprawdzi Pani to równanie 22:00 ?

Eta: Jest ok

	π		π		5
lub można x= −		+2kπ= 2π−		+2kπ=		π+2kπ, k∊C
	3		3		3

nie zapominaj pisać, że k∊C !

Radek: Dziękuję, teraz idę na kolację ale jeszcze mam trochę zadań i liczę na Panią !

Eta: Ja też idę..................... ( na kolację