Określ czy wykresy funkcji się przecinają
Radek: Witam mam takei zadanie określ czy proste są prostymi przecinającymi się gdy:
| | x+3 | | 1 | |
f(x)= |
| i g(x)=4+ |
| x |
| | 4 | | 4 | |
Pomoże ktoś?
7 gru 17:33
krystek: Gdy nie są równoległe lub nakładaja się . Popatrz na współczynniki kierunkowe
7 gru 17:34
Radek: Równoległe są gdy a1=a2
Wiem że w g(x) a=1/4x a w f(x) jak wyznaczyc a ? 1/4x tez ?
7 gru 17:40
Radek: Czyli przecinają się gdy nie są równoległe oraz gdy nie nakładają się ? A kiedy się nakładają ?
7 gru 17:47
5-latek: | | x+3 | | x | | 3 | | 1 | | 3 | |
f(x)= |
| to f(x)= |
| + |
| to f(x)= |
| x+ |
| i teraz sobie porownaj f(x) z |
| | 4 | | 4 | | 4 | | 4 | | 4 | |
g(x)
7 gru 17:49
5-latek: Nakladaja sie kiedy maja te same rownania
7 gru 17:49
bezendu:
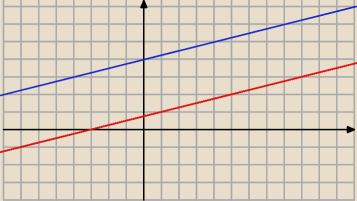
7 gru 17:50
Janek191:
| | x + 3 | | 1 | | 3 | |
f(x) = |
| = |
| x + |
| |
| | 4 | | 4 | | 4 | |
| | 1 | | 1 | |
g(x) = 4 + |
| x = |
| x + 4 |
| | 4 | | 4 | |
a
1 = a
2
Proste są równoległe

7 gru 17:51
Radek: Czyli nie przecinają się gdy nie są równoległe i gdy nie nakładają się ?
Dzięki
7 gru 17:54
5-latek: zle myslisz . Nie przecinaje sie gdy sa rownolegle lub nakladaja sie na siebie
7 gru 18:20

