.
Piotr 10: Dwie proste równoległe k i l leżą na płaszczyźnie π w odległości 28 cm od siebie. Prosta m,
leżąca poza płaszczyzną, jest równoległa do prostej k i oddalona od niej o 17cm , a od
płaszczyzny π o 15cm. Oblicz odległość między prostymi m i l.
Bardzo proszę o wyjaśnienie mi tego zadania
7 gru 16:25
Mila:
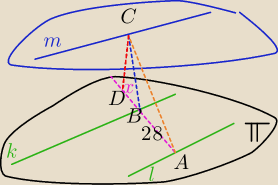
I przypadek spodek wysokości CD leży przed prostą k
CD⊥AB,
CD=15 cm
BC=17 cm
AC=?
15
2+x
2=17
2
x=8
W ΔCDA:
|AC|
2=|CD|
2+(x+BA)
2
|AC|
2=15
2+(8+28)
2
|AC|
2=225+1296
|AC|
2=1521
|AC|=39cm
II przypadek
Spodek wysokości CD leży między punktami A i B
Dokończysz?
7 gru 16:51
Janek191:
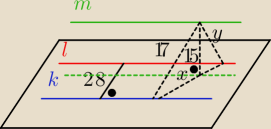
Mamy
x
2 + 15
2 = 17
2
x
2 + 225 = 289
x
2 = 289 − 225 = 64
x = 8
−−−
oraz
( 20 − x)
2 + 15
2 = y
2
y
2 = 12
2 + 15
2 = 144 + 225 = 369
y =
√369 = 3
√ 41
=============
d( m, l ) = 3
√41 cm
7 gru 17:05
Piotr 10: Ok, dziękuje wam

.
Mila mam pytanie: Czy zadania tego typu mogą wystąpić na maturze? I
czy zadania z działu ''Płaszczyzny i proste w przestrzeni. Rzut prostokątny na płaszczyznę'' z
zbioru Pazdro też mogą wystąpić czy nie?
7 gru 19:56
pigor: ...,
Janek... bład nieuwagi (znam to)

nie 20−x, tylko 28−x= 20 .
7 gru 20:09
 I przypadek spodek wysokości CD leży przed prostą k
CD⊥AB,
CD=15 cm
BC=17 cm
AC=?
152+x2=172
x=8
W ΔCDA:
|AC|2=|CD|2+(x+BA)2
|AC|2=152+(8+28)2
|AC|2=225+1296
|AC|2=1521
|AC|=39cm
II przypadek
Spodek wysokości CD leży między punktami A i B
Dokończysz?
I przypadek spodek wysokości CD leży przed prostą k
CD⊥AB,
CD=15 cm
BC=17 cm
AC=?
152+x2=172
x=8
W ΔCDA:
|AC|2=|CD|2+(x+BA)2
|AC|2=152+(8+28)2
|AC|2=225+1296
|AC|2=1521
|AC|=39cm
II przypadek
Spodek wysokości CD leży między punktami A i B
Dokończysz?
 Mamy
x2 + 152 = 172
x2 + 225 = 289
x2 = 289 − 225 = 64
x = 8
−−−
oraz
( 20 − x)2 + 152 = y2
y2 = 122 + 152 = 144 + 225 = 369
y = √369 = 3 √ 41
=============
d( m, l ) = 3√41 cm
Mamy
x2 + 152 = 172
x2 + 225 = 289
x2 = 289 − 225 = 64
x = 8
−−−
oraz
( 20 − x)2 + 152 = y2
y2 = 122 + 152 = 144 + 225 = 369
y = √369 = 3 √ 41
=============
d( m, l ) = 3√41 cm
 . Mila mam pytanie: Czy zadania tego typu mogą wystąpić na maturze? I
czy zadania z działu ''Płaszczyzny i proste w przestrzeni. Rzut prostokątny na płaszczyznę'' z
zbioru Pazdro też mogą wystąpić czy nie?
. Mila mam pytanie: Czy zadania tego typu mogą wystąpić na maturze? I
czy zadania z działu ''Płaszczyzny i proste w przestrzeni. Rzut prostokątny na płaszczyznę'' z
zbioru Pazdro też mogą wystąpić czy nie?
 nie 20−x, tylko 28−x= 20 .
nie 20−x, tylko 28−x= 20 .