dziedzina renia: Wyznacz dziedzine: f(x) = ln (2x²−5x−3) / ( 1−x)

5-latek: 1−x≠0 i 2x²−5x−3>0 a to juz studentka rozwiaze

renia: hmm.. wątpie :c

5-latek: Mam nadzieje z eto jest zart z Twojej strony

renia: obliczyłam tylko nie wiem co z tym zrobic

5-latek: To napisz co wyszlo

renia: 2x2−5x−3>0 x1= 1 i x2 = 1 ¹₂

5-latek: NO to w jkim przedziale bedzie to >0 ? i drugi warunek 1−x≠0 to x≠ ile i potem dziezdzina to ten wlasnie przedzial minus to co z drudgiego warunku

renia: 2x2−5x−3>0 x1= 1 i x2 = 1 ¹₂ [1;1¹₂] 1−x≠0 x=1 Df = [1;1¹₂] / 1 = 1¹₂

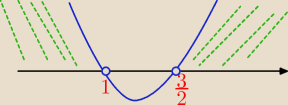
Hajtowy: Tak więc?

renia: skąd te ³₂ ?

renia: dobra nie było pytania

Hajtowy: 2x²−5x−3 > 0 Δ=25+24=49 √Δ=7

	5−7		2		1
x1=		=−		=−
	4		4		2

	5+7		12
x2=		=		=3
	4		4

Tak więc jak to możliwe, że u Cb pierwiastki wyszły 1 oraz 1,5 ? x=−0,5 v x=3 Innej opcji nie ma... Teraz rysunek, jeśli nie widzisz rozwiązania. Rozwiązanie uwzględnij z dziedziną!

5-latek: To naprawde nie byl zart Ty naprawde nie umiesz Nie dosc ze nie taki przedzial bo otwarty to jeszce w tym przedziale jest <0 to do tego zle policzone miejsca zerowe

	1
ma byc x1=−		i x2=3 ,
	2

	1
I teraz 2x2−5x−3>0 gdy x nalezy (−oo ,−		)U(3,oo) i uwzgledniajac drugi warunek
	2

D_f=(−oo,−1/2)U(3,oo)\1 a toD_f=(−oo,−1/2)U(3,oo) Jak Ty zdalas mature

Hajtowy: 5−latku

renia: aaaaaa ok czyli df=(−∞; ¹₂) u [ 3;+∞)

5-latek: Czesc . Tylko nie wiadomo czy sie smiac z tego czy plakac

renia: tyle że ja jeszcze nie pisałam matury

5-latek: Popraw to napisalem CI jak dziedzina . Zwrot nierownosci jest taki > a nie ≥

renia: dzieki wam

5-latek: Calusa przyjme I pocwicz wiecej przykladow .Dobrze?