Znajdź równanie okręgu opisanego na trójkącie o wierzchołkach A=(1,5), B=(8,-2) kamczatka: Znajdź równanie okręgu opisanego na trójkącie o wierzchołkach A=(1,5), B=(8,−2) i C=(9,1) Trzeba wyznaczyć punkt przecięcia symetralnych jego boków i mam pytanie obojętnie które to boki mogą być ? np może być symetralna A i B czy A i C ? Które boki brać do wyznaczania tej symetrlanej ?

Mila: Wybierasz dwa dowolne boki, bo symetralne boków Δ przecinają się w jednym punkcie.

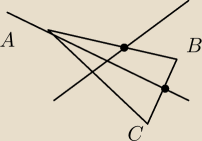
kamczatka: to tutaj przecież symetralna boku A i B mają inny punkt przecięcia niż symetralna boku BC

kamczatka: czy tu chodzi o punkt przecięcia symetralnych ?

kamczatka: dobra to już wiem

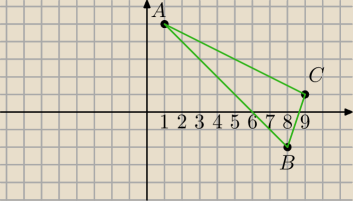
Mila: Chodzi o przecięcie się symetralnych ze sobą a nie z bokami. A=(1,5), B=(8,−2) i C=(9,1) Lepiej skorzystaj z wzoru: S=(a,b) środek okręgu (x−a)²+(y−b)²=r² równanie okręgu ośrodku S i promieniu r. Podstawiając wsp. punktów A,B,C mamy: (1−a)²+(5−b)²=r² (8−a)²+(−2−b)²=r² (9−a)²+(1−b)²=r² Rozwiń wg wzorów skróconego mnożenia i odejmij równania stronami. Dokończ.

kamczatka: i co z tych równań ma wyjść ?

kamczatka: np. z pierwszego równania wychodzi a²−2a+26−10b+b²=r² i co dalej

kamczatka: ?

kamczatka: dobra już wiem

kamczatka: a by mógł mi ktoś pomóc wyznaczyć równanie symetralnej BC ? Prosta BC: −2=8a+b 1=9a+b a=3 b=−26 więc równanie prostej BC : y=3x−26

	1
xs=8
	2

	1
ys=−
	2

	1		1
S=(8		),−		)
	2		2

Symetralna

	1
y=−		+b
	3

I mi tu właśnie coś nie wychodzi dobrze robiłem do tej pory?

kamczatka: dobra zrobiłem