Błagam POMOCY!!!!
kat_e: Błagam POMOCY


Odcinek AB jest średnicą okręgu o opisanego na czworokącie wypukłym ABCD , którego przekątne
przecinają się w punkcie E . Proste styczne do okręgu o w punktach C i D przecinają się w
punkcie P .
Udowodnić, że PC = PE .
Rozwiązanie Niech Q będzie punktem przecięcia prostych AD i BC .
Zauważmy najpierw, że na mocy warunków zadania proste AC i BD są wysokościami trójkąta ABQ .
Zatem prosta QE jest jego trzecią wysokością i wobec tego przecina prostą AB w pewnym punkcie
F pod kątem prostym.
1.W trójkącie ECQ kąt przy wierzchołku C jest prosty, a środek P' odcinka QE jest środkiem
przeciwprostokątnej. Stąd uzyskujemy zależności ∡ P'CQ=∡ P'QC =∡ FQB . Ponadto trójkąty
prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B , zatem ich pozostałe kąty
ostre są równe: ∡ FQB = ∡ CAB . Udowodniliśmy tym samym, że ∡ P'CQ = ∡ CAB To oznacza, że
prosta P'C jest styczna do okręgu o w punkcie C .
2. Podobnie dowodzimy, że prosta P'D jest styczna do okręgu o w punkcie D . Stąd i z określenia
punktu P wynika, że P'=P . Innymi słowy, punkt P jest środkiem przeciwprostokątnej w trójkącie
prostokątnym ECQ , skąd natychmiast wynika żądana równość PC = PE
6 gru 13:38
wredulus_pospolitus:
i jakiej od nas pomocy oczekujesz

byś przynajmniej zrobiła rysunki odpowiednie tutaj
6 gru 13:38
wredulus_pospolitus:
" Odcinek AB jest średnicą okręgu o opisanego na czworokącie wypukłym ABCD , którego przekątne
przecinają się w punkcie E . Proste styczne do okręgu o w punktach C i D przecinają się w
punkcie P .
Udowodnić, że PC = PE "
Informacja o tym, że AB jest średnią −−− zmylka ... nie potrzebujesz tego
zadanie sprowadza się do rysunku ... zaznaczenia OC,CP,PE,EO oraz OP
pokazania, że trójkąty są przystające
6 gru 13:41
wredulus_pospolitus:
ach ... nie doczytałem

6 gru 13:42
kat_e: proszę tylko o wytłumaczenie z jakich zależności to wynika...
staram się zrobić rysunek, ale trochę czasu mi to zajmie
6 gru 13:42
kat_e: dziękuję

6 gru 13:45
kat_e: Rozumiem że to wszystko w tym temacie

?
czy nadal wklejać rysunek

?
6 gru 13:49
wredulus_pospolitus:
dawaj rysunek ... bo mi się tego nie chce rysować

6 gru 13:50
wredulus_pospolitus:
Zacznijmy od tego, że musisz zauważyć, że kąty wewnętrzne przy C i D to kąty proste

I stąd masz wiedzę o tym że AC i BD są wysokościami tamtego trójkąta
a skąd wiesz że tam są kąty proste

tw. o kątach opartych na tym samym łuku

6 gru 13:55
kat_e:
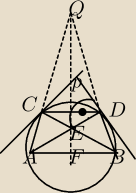
6 gru 14:01
kat_e: ok...... przepraszam, że ten rysunek tak wygląda, ale lepiej nie potrafiłam

6 gru 14:03
kat_e: błąd C musi być w miejscu D
6 gru 14:06
kat_e: Tak dotarłam już do tego. Podobnie będzie w ostatniej części zadania. Ale dlaczego: ECQ kąt
przy wierzchołku C jest prosty (no to już wiem), a środek P' odcinka QE jest środkiem
przeciwprostokątnej ( to też jest dla mnie jasne) Stąd uzyskujemy zależności ∡ P'CQ=∡ P'QC =∡
FQB (

). Ponadto trójkąty prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B ,
zatem ich pozostałe kąty ostre są równe: ∡ FQB = ∡ CAB (ale to

)
6 gru 14:47

 Odcinek AB jest średnicą okręgu o opisanego na czworokącie wypukłym ABCD , którego przekątne
przecinają się w punkcie E . Proste styczne do okręgu o w punktach C i D przecinają się w
punkcie P .
Udowodnić, że PC = PE .
Rozwiązanie Niech Q będzie punktem przecięcia prostych AD i BC .
Zauważmy najpierw, że na mocy warunków zadania proste AC i BD są wysokościami trójkąta ABQ .
Zatem prosta QE jest jego trzecią wysokością i wobec tego przecina prostą AB w pewnym punkcie
F pod kątem prostym.
1.W trójkącie ECQ kąt przy wierzchołku C jest prosty, a środek P' odcinka QE jest środkiem
przeciwprostokątnej. Stąd uzyskujemy zależności ∡ P'CQ=∡ P'QC =∡ FQB . Ponadto trójkąty
prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B , zatem ich pozostałe kąty
ostre są równe: ∡ FQB = ∡ CAB . Udowodniliśmy tym samym, że ∡ P'CQ = ∡ CAB To oznacza, że
prosta P'C jest styczna do okręgu o w punkcie C .
2. Podobnie dowodzimy, że prosta P'D jest styczna do okręgu o w punkcie D . Stąd i z określenia
punktu P wynika, że P'=P . Innymi słowy, punkt P jest środkiem przeciwprostokątnej w trójkącie
prostokątnym ECQ , skąd natychmiast wynika żądana równość PC = PE
Odcinek AB jest średnicą okręgu o opisanego na czworokącie wypukłym ABCD , którego przekątne
przecinają się w punkcie E . Proste styczne do okręgu o w punktach C i D przecinają się w
punkcie P .
Udowodnić, że PC = PE .
Rozwiązanie Niech Q będzie punktem przecięcia prostych AD i BC .
Zauważmy najpierw, że na mocy warunków zadania proste AC i BD są wysokościami trójkąta ABQ .
Zatem prosta QE jest jego trzecią wysokością i wobec tego przecina prostą AB w pewnym punkcie
F pod kątem prostym.
1.W trójkącie ECQ kąt przy wierzchołku C jest prosty, a środek P' odcinka QE jest środkiem
przeciwprostokątnej. Stąd uzyskujemy zależności ∡ P'CQ=∡ P'QC =∡ FQB . Ponadto trójkąty
prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B , zatem ich pozostałe kąty
ostre są równe: ∡ FQB = ∡ CAB . Udowodniliśmy tym samym, że ∡ P'CQ = ∡ CAB To oznacza, że
prosta P'C jest styczna do okręgu o w punkcie C .
2. Podobnie dowodzimy, że prosta P'D jest styczna do okręgu o w punkcie D . Stąd i z określenia
punktu P wynika, że P'=P . Innymi słowy, punkt P jest środkiem przeciwprostokątnej w trójkącie
prostokątnym ECQ , skąd natychmiast wynika żądana równość PC = PE
 byś przynajmniej zrobiła rysunki odpowiednie tutaj
byś przynajmniej zrobiła rysunki odpowiednie tutaj


 ?
czy nadal wklejać rysunek
?
czy nadal wklejać rysunek ?
?

 I stąd masz wiedzę o tym że AC i BD są wysokościami tamtego trójkąta
a skąd wiesz że tam są kąty proste
I stąd masz wiedzę o tym że AC i BD są wysokościami tamtego trójkąta
a skąd wiesz że tam są kąty proste  tw. o kątach opartych na tym samym łuku
tw. o kątach opartych na tym samym łuku 


 ). Ponadto trójkąty prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B ,
zatem ich pozostałe kąty ostre są równe: ∡ FQB = ∡ CAB (ale to
). Ponadto trójkąty prostokątne ACB i QFB mają wspólny kąt ostry przy wierzchołku B ,
zatem ich pozostałe kąty ostre są równe: ∡ FQB = ∡ CAB (ale to  )
)