Wykres funkcji Albert:

	3x+2
Wykres funkcji g jest symetryczny do wykresu funkcji f(x)=−		względem prostej o
	x+2

	a
podanym równaniu. Zapisz jej wzór w postaci g(x)=		+q
	x−p

a) względem prostej x=−2 proszę o wskazówkę robiąc g(x)=f(−2x) to dobry pomysł?

Albert:

wredulus_pospolitus: 1) przekształć widoczną postać f(x) w taką jakiej postaci szukasz g(x) 2) zauważ, ze D_f = R/{−2} 3) tak więc, g(x) jest symetryczna względem asymptoty pionowej funkcji f(x) 4) jak w takim razie będzie wyglądał wykres g(x) 5) koniec zadania

Albert: to jest LO nie miałem przebiegu zmienności i nie umeim i nie che umieć wzoru na asymptoty xd

Albert: wiem, że wykres będzie taki sam ale jak byłoby wzg. prostej x=−3 to jak to przekształcić?

wredulus_pospolitus: to że nie masz wyznaczania asymptot w liceum nie oznacza, że jesteś zwolniony z takiej wiedzy jak: hiperbola posiada dwie asymptoty i potrafienia ich wyznaczania (co de facto pozwala narysować daną hiperbolę) i nie ... wykres nie będzie taki sam gdyby funkcja g(x) była symetryczna względem np. x=−3 to ... graficznie najszybciej by się do tego doszło jak wygląda nowy wykres

Albert: wiem ale muszę podać wzór, W takim razie nie czaje

Albert: dlaczego nie tak samo jak asymptota pionowa jest równa −2 to jest ten sam wykres.

wredulus_pospolitus:

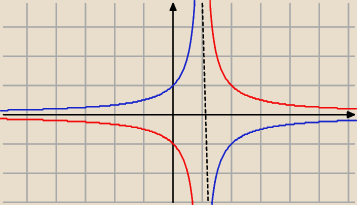
	1
analogiczny przykład ale z funkcją f(x) =
	x−1

asymptota pionowa x=1 g(x) jest symetryczna z f(x) względem x=1

Albert: a bez takiej interpretacji graficznej jak to wyznaczyc?

Albert: a co do tego zadania to mam względem prostej x=−2

	−4
f(x) po przekształceniu wyszło:		−3
	x+2

i taka też jest odpowiedź, że tak ma wyglądać funkcja g(x)

wredulus_pospolitus: hmmm ogólny przypadek dla każdej osi symetrii − nie musi to być któraś z asymptot (tylko dla hiperbol): 1) znaleźć punkt przecięcia się osi symetrii z asymptotą 2) wyznaczyć wektor o jaki trzeba przesunąć wykres aby ten punkt znalazł się w (0,0) 3) znaleźć wzór funkcji f₁(x) (czyli f(x) po tym właśnie przesunięciu) 4) dokonać przekształcenia wedle osi symetrii (w 99% przypadków będzie to OX ... czyli robisz g₁(x) = f₁(−x) ) 5) przesuwasz wykres g₁(x) o wektor wyznaczony w punkcie (2) koooniec

wredulus_pospolitus: jeżeli osią symetrii jest jedna z asymptot to w takiej postaci f(x) po prostu 'wrzucasz' − przed ułamek

wredulus_pospolitus: czyli:

	+4
g(x) =		−3
	x+2

Albert: a co do tego zadania to mam względem prostej x=−2 f(x) po przekształceniu wyszło:

	−4
		−3
	x+2

i taka też jest odpowiedź, że tak ma wyglądać funkcja g(x)

Albert:

	−4
a ja mam w odp że g(x) jest		−3
	x+2

wredulus_pospolitus: jeżeli oś symetrii nie pokrywa się z żadną z asymptot to masz trudniejsze zadanie i musisz zrobić jak napisałem o 12:53 ... ponieważ symetria powoduje 'zmianę' położenia którejś (przynajmniej jednej) asymptoty (tej która nie jest równoległa do osi symetrii danej w zadaniu)

wredulus_pospolitus: bo masz błąd w f(x)

	3x+2		3x+6 − 4		−4		+4
f(x) = −		= −		= −		− 3 =		− 3
	x+2		x+2		x+2		x+2

Albert:

	3x+2
nie rozumie dalej dlaczego funkcja f(x)=−		po odbiciu wzg prostej x=−2 jest równa
	x+2

−4
	−3
x+2

Albert: aha dzięki wielkie

wredulus_pospolitus: Albert zauważ, że:

	4
f(x) =		− 3
	x+2

	4
to +2 i −3 to jest de facto "pozostałość po"/"informacja o" wektorze, który przesunął
	x

do takiej właśnie pozycji szukasz funkcji g(x) symetrycznej względem jednej z asymptot ... czyli asymptoty pozostaną w tym samym miejscu ... więc "pozostałość po"/"informacja o" wektorze będzie taka sama

	4		4		−4
symetryczny wykres do		względem asymptoty to będzie −		... czyli		...
	x		x		x

	−4
przesuwasz go o wspomiany wektor i powstaje:		− 3
	x+2

wredulus_pospolitus: gdyby osią symetrii była inna prosta (dla uproszenia nadal byłaby to prosta równoległa do

	−4
którejś asymptoty) to doszłoby do zmiany 'informacji o' wektorze który przesunąłby		w
	x

odpowiednie miejsce (punkt przecięcia się asymptot by się zmienił)

wredulus_pospolitus: na dobrą sprawę ... bez wyobrażenia sobie tego graficznie −−−−− baaaaaardzo ciężko by było to rozwiązać

Albert: z postu o 12:53 5) przesuwasz wykres g₁(x) o wektor wyznaczony w punkcie (2) tylko że współrzędne wektora mają być przeciwnych znaków niż wyznaczony tak?

Albert: a jak jest względem y=−x−5 to przesuwamy na punkt [0;0] i odbijamy wzoględem punktu (0;0) −f(−x) tak?

wredulus_pospolitus: niee ... współrzędne mają być takie same

wredulus_pospolitus: bo te współrzedne wektora reprezentują jedyny punkt przecięcia sie osi symetrii z asymptotą ... czyli punkt który 'pozostanie na swoim miejscu'

wredulus_pospolitus: względem y=−x−5 szczerze mówiąc ... zycze powodzenia w próbie tego zrobienia ... na dobrą sprawę ... aby szybko i sprawnie zrobić symetrię ... nalezy zacząć od wskazania nowego miejsca przecięcia się asymptot (i wykreślenia ich) reszta to już idzie 'jak z bicza strzelił' co więcej ... mając (nowe) współrzedne punktu przeciecia się asymptot ... znasz wektor o który musisz przesunąć funkcję g₁(x) = −f₁(x)