tryg
Radek:
Jak rozwiązać takie równanie
sinx=0
x=0+2kπ
x=2kπ ?
5 gru 23:55
ZKS:
sin(x) przecina oś OX co π.
5 gru 23:57
Janek191:
x = k*π , k − dowolna liczba całkowita
5 gru 23:57
Radek:
x=kπ k∊C ?
5 gru 23:58
Radek:
ZKS a w książce mam podane, że x=2kπ
tak samo
sinx=1
6 gru 00:04
ZKS:
Ale przecież sin(x) = 1 jest dobrze rozwiązany bo sin(x) w swoim okresie tylko raz
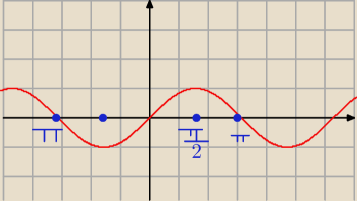
się styka z 1. Natomiast jeżeli masz równanie sin(x) = 0 to sinus w swoim okresie przecina
oś OX co π spójrz na rysunek.
6 gru 00:08
Radek:
6 gru 00:10
Radek:
to jest jakiś wyjątek ? sinx=0 ?
6 gru 00:13
ZKS:
I tutaj właśnie widać że sin(x) przecina oś OX co π natomiast sin(x) = 1 osiąga tylko raz w
swoim okresie.
6 gru 00:14
ZKS:
Jaki wyjątek?
6 gru 00:16
Radek:
ZKS czyli sinx=0 to jest tak jakby wyjątek bo dla sin jest 2kπ ?
6 gru 00:16
Radek:
Zawsze w tych równaniach jak mieliśmy sin to pisaliśmy +2kπ k∊C a nie kπ
6 gru 00:17
ZKS:
Nie to nie jest żaden wyjątek. Możesz też rozwiązać tak
sin(x) = 0
x = k * 2π ∨ x = π + k * 2π tutaj widać że te rozwiązanie można zapisać jako jedno
x = k * π ponieważ te rozwiązania powtarzają się co π.
Rozumiesz?
6 gru 00:19
Radek:
Nie było pytania
już wiem patrząc na wykres wszystko skumałem
po okres podstawowy to 2π
Dzięki za pomoc i dobranoc
Mam nadzieję, że jutro mi pomożesz w trudniejszych równaniach !
6 gru 00:20
ZKS:
Jeżeli choroba mnie do końca nie rozłoży to powinienem jutro być na forum.
Nie ma za co i dobranoc.
6 gru 00:23
Radek: To wracaj do zdrowia !
6 gru 00:24
ZKS:
Dziękuję postaram się.
6 gru 00:27