Stereometria Adrian: Pilnie potrzebuję rozwiązania tego jeszcze przed jutrem! Oblicz promień kuli wpisanej w ostrosłup prawidłowy czworokatny o krawędzi podstawy a i kącie płaskim przy wierzchołku α

Adrian: UP

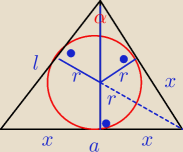Janek191: Dane: a , α x = 0,5 a

x		r
	=
h		l − x

x
	= tg 0,5 α ⇒ x = h*tg 0,5 α ⇒ 0,5 a = h*tg 0,5 α ⇒ a = 2 h*tg 0,5 α
h

	a
h =
	2 tg 0,5 α

−−−−−−−−−−−−− oraz

	a2		a2		1
l2 = x2 + h2 = (0,5 a)2 +		=		*(1 +		)
	4 tg2 0,5 α		4		tg2 0,5 α

	a		1
l =		√ 1 +
	2		tg2 0,5 α

zatem

0,5 a		r
	=
a     2 tg 0,5α		1   0,5a*√ 1 + − 0,5 a   tg2 0,5α

	2r
tg 0,5 α =
	1   a*√ 1 + − a   tg2 0,5α

	1
2 r =a *tg 0,5 α ( √ 1 +		− 1)
	tg2 0,5 α

	1
r = 0,5 a* tg 0,5 α *( √ 1 +		− 1)
	tg2 0,5 α

======================================

	1
Pod znakiem pierwiastka jest 1 +
	tg2 0,5 α