Wyznacz najmniejszą i największą wartość funkcji Maciek: Wyznacz najmniejszą i największą wartość funkcji:

	x−5
f(x)=		w przedziale x∊[0,4]
	x−6

obliczam pochodną ale nie chce mi wyjść..

	1*(x−6)−(x−5)*1))		−1
f '(x)=		=
	(x−6)2		(x−6)2

i jak chcę przyrównać do zera to wychodzi takie coś..:

−1
	=0
(x−6)2

−1=0

daras: pochodna nie ma miejsc zerowych, bo to funkcja homo sprawdź wartości funkcji na końcach przedziału

wredulus_pospolitus: no i co związku z tym jaki wniosek wysnuwasz dla jakiego argumentu będzie wartość największą a dla jakiego najmniejszą

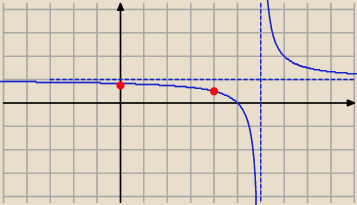
Bogdan: To funkcja homograficzna, malejąca w przedziałach: (−∞, 6), (6, +∞). . Dla x∊<0, 4) największa wartość to f(0), najmniejsza to f(4)

Bogdan: Dla x∊<0, 4>

daras: a Maćka juz dawno to nie interesuje