pochodne/ekstrema student: Znajdź ekstrema i przedziały monotoniczności dla funkcji:

	x+2
y=
	x2+1

wredulus_pospolitus: 1) D_f = .... 2) f'(x) = .... 3) wyznaczasz przedziały monotoniczności

student: Df=R\{−1,1}

	−x2−4x−1
f'(x)=
	(x−1)(x−1)

miejsca zerowe x₁= −2+√3 x₂=−2−√3 a kiedy rośnie kiedy maleje bo nie wiem

wredulus_pospolitus: Skąd taka pochodna Ci wyszła

wredulus_pospolitus: i jak z x²+ 1 wyszło Ci (x−1)(x−1) = (x−1)² = x²−2x+1

student:

−x2−4x−1
(x2−1)2

chyba tak powinno być

student: sorki błąd jak przepisywałem + źle na początku poprawiłem już

student: a jak wyznaczyć kiedy f rośnie, maleje, jakie ma maksimum

wredulus_pospolitus: na podstawie znaku pochodnej jeżeli f'(x) > 0 to f(x) rosnąca jeżeli f'(x) < 0 to f(x) malejąca jeżeli f'(x) = 0 to MOŻE być tutaj maksimum/minimum (warunek konieczny, ale niewystarczający)

student: ok więc w tym wypadku f'(x)<0 więc f(x) malejąca a teraz na jakim przedziale? na (−2−√3, −2+√3) maleje a rośnie na jakimś? i gdzie maksimum

wredulus_pospolitus: student −−− byłeś na zajęciach uważałeś na ćwiczeniach

student: no jasne że byłem, tylko 1 przykład przerobiliśmy i nic z niego zbytnio wynieść nie mogę

wredulus_pospolitus: błąd w pochodnej 1*(x²+1) − (x+2)*(2x) = x² + 1 − 2x² − 4x = −x² − 4x + 1

student: ok tak

student: a możesz napisać jakie są przedziały?, gdy bd chociaż w 1 przykładzie rozumiał, zrobię kolejne 3 inaczej stoję w miejscu

student: .

student: .

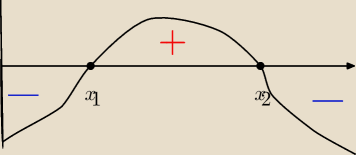
wredulus_pospolitus: −x²−4x+1 = 0 ⇔ x = −2−√5 lub x = −2 + √5 rysujesz szkic wykresu pochodnej (patrz rysunek) jak narysowac chyba wiesz −−− to było w liceum (jeżeli nie w gimnazjum) ze szkicu od razu widać monotoniczność funkcji f(x)

wredulus_pospolitus: ekstrema −−− ekstrema są w miejscach zerowych f'(x) ... gdy dodatkowo pochodna 'zmienia' znak w otoczeniu tegoż miejsca zerowego w tym przypadku są dwa ekstrema −−− x₁ i x₂ x₁ to jest minimum ... ponieważ funkcja 'maleje maleje maleje ... ekstremum ... zaczyna rosnąć) x₂ to jest maksimum ... ponieważ funkcja 'rośnie rośnie rośnie ... ekstremum ... zaczyna maleć)

student: super! dziękuję

Jolanta: a dlaczego w dziedzinie nie ma x∊R

wredulus_pospolitus: no tak ... zapomniałem ... na szkicu f'(x) 'kółkami' zaznacza się punkty wypadające z dziedziny

student: jest Df=R\{−1,1} czyli rzeczywiste za wyjątkiem −1 i 1

wredulus_pospolitus: Jolanta ... bo w mianowniku jest x²−1

student: aha czyli kółka otwarte mają być?