Rozwiąż równanie wajdzik: Rozwiąż równanie

	x		x
ctg2		−ctg		=0
	8		8

	x
ctg		(ctg−1)=0
	8

Nie za bardzo tutaj wszystko rozumiem, zacznijmy od tego, czy mogę tak wyciągnąć przed nawias "to" wyrażenie?

Bizon: −OCZYWIŚCIE MOŻESZ tylko przy drugim ctg opuściłeś kąt −

wajdzik: no tak, zgadza się, mam napisać tam "ctgx"?

Bizon: NIE

Bizon:

	x		x		x		x
ctg2		−ctg		=ctg		(ctg		−1)
	8		8		8		8

wajdzik: Nie wiem jak mogę być tak nieuważny. a więc rozwiązuję:

wajdzik:

x		π
	=		+2kπ //*8
8		4

x=2π+8kπ x=2π(1+4k) i teraz II przypadek

wajdzik:

	π		π
−		=
	4		2

x		π
	=		+kπ
8		2

x=4π+8kπ x=4π(1+2k) A we wcześniejszym przykładzie jest błąd w 1 linijce bo ma być "kπ"

wajdzik: Zgadza się? Więc: x=2π(1+4k) V x=4π(1+2k), k∊C

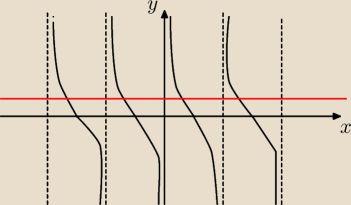
Bizon: oj wajdzik ... a jakiż to jest okres cotangensa ? − Pora na wietrzenie pokoju −

wajdzik: T=π ... tak?

wajdzik: nigdy nie lubiłem odczytywać z wykresu − bo tego nie rozumiałem

wajdzik:

	x
Inaczej, ctg		=0
	8

Bizon: ... Zastanów się co robimy wcześniej: a) ustalamy kąt ... a później rozszerzamy o okres

	x
czyli ctg		=1
	8

x/8= ... ⇒ x= .... x= ...+kπ b) czy tak ja zrobiłeś ? I jaką to czyni różnicę

wajdzik: czyli wtedy mamy:

x		π
	=		+kπ
8		2

x=4π+8kπ x=4π(1+2k) x=2π(1+4k) V x=4π(1+2k), k∊C Dobrze to widzę

wajdzik:

	π
x/8=		+kπ ⇒ x=2π+8kπ x=2π(1+4k)
	4

	π
x/8=		+kπ ⇒ x=4π+8kπ x=4π(1+2k)
	2

Ja to rozumuję tak

wajdzik: czyli to co ja napisałem jest niewystarczające?

wajdzik:

wajdzik:

wajdzik:

wajdzik:

Bizon: ... to jaki wynik zapiszesz?

wajdzik: x=2π(1+4k) V x=4π(1+2k), k∊C